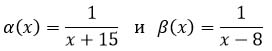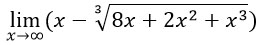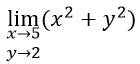Даны две бесконечно малые при x→∞ α(х)=1/(х+15) и β(х)=1/(х-8). Приведите расчеты, показывающие их эквивалентность.

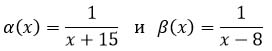
Бесконечно малые в некоторой точке функции называются эквивалентными, если 

Проверяем.

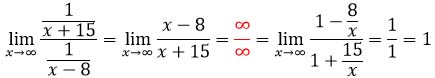
Значит, функции эквивалентны, т.е. α(x) ~ β(x).

Комментарий. Неопределенность вида ∞/∞ раскрывается делением числителя и знаменателя на икс в старшей степени. В данном случае делить мы будем просто на икс. Единицы в числителе и знаменателе стремятся к 1, а дроби стремятся к нулю, т.к. подставляя вместо икс бесконечность, получаем, что числа 8 и 15 делятся на бесконечно большое число. А чем больше знаменатель, тем меньше результат деления.