Даны n различных натуральных чисел, составляющих арифметическую прогрессию, причем n>=3. а) Может ли сумма всех данных чисел быть равной 15? б) Найдите все значения n, если сумма всех данных чисел равна 51.

n - количество членов арифметической прогрессии.

а) Чтобы ответить на первый вопрос достаточно подобрать несколько чисел таким образом, чтобы в сумме они давали 15 (причем их количество как минимум равно трем). Не забываем, что у нас арифметическая прогрессия, значит, эти числа увеличиваются на одно и тоже число.

Если сложить числа 4, 5 и 6, то в сумме они равны 15. Эти числа составляют арифметическую прогрессию с разностью d = 1.

б) Вспомним формулу суммы первых n членов арифметической прогрессии и выразим из нее сумму первого и последнего члена.

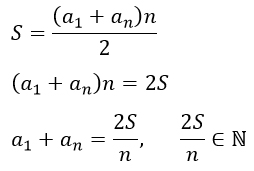
Обратите внимание, что 2S/n является натуральным, т.к. складываем мы натуральные числа.

По условию задачи, сумма чисел равна 51, т.е.

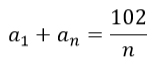
Число 102 нацело делится на n = 1; 2; 3; 6; 17; 34; 51; 102.

n = 1 и n = 2 можем сразу откинуть, т.к. n ≥ 3.

Если n = 3, то а₁ + а_n = 34. Подберем три таких числа а₁, а₂ и а₃, чтобы а₁ + а₂ + а₃ = 51 и а₁ + а₃ = 34:      3, 17, 31.

Если n = 6, то а₁ + а_n = 17. Подберем шесть таких чисел а₁, а₂, а₃, а₄, а₅ и а₆ чтобы а₁ + а₂ + а₃ + а₄ + а₅ + а₆ = 51 и а₁ + а₆ = 17:       6, 7, 8, 9, 10, 11.

Если n = 17, то а₁ + а_n = 6. В этом случае мы не сможем подобрать 17 натуральных чисел таким образом, чтобы в сумме они давали 6. Аналогично при n = 34; 51; 102.

Ответ: а) да, например, 4, 5, 6;   б) n = 3, n = 6.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.