-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
Обозначим оценки кинокритиков как а1, а2, а3, а4, а5, причем а4 – минимальная оценка, а5 – максимальная.
Запишем формулу для нахождения рейтинга сериала на первом сайте:
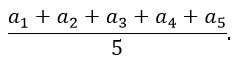
И запишем формулу для нахождения рейтинга на втором сайте:
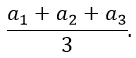
Разность этих рейтингов должна равняться 1/15, т.е.
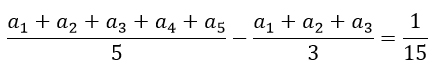
Преобразуем равенство.
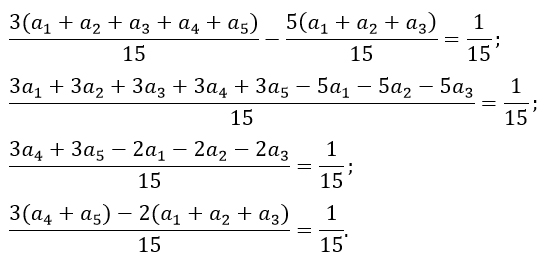
Чтобы это равенство выполнялось надо, чтобы числитель был равен 1.
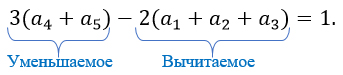
Вычитаемое представляет собой четное число потому, что какое бы число не стояло в скобках, оно умножается на 2.
Поэтому, чтобы разность равнялась единице надо, чтобы уменьшаемое было нечетным.
Ничего кроме подбора в голову не приходит. Попробуем в первые скобки подставить числа 1 и 10, тогда уменьшаемое будет равно 33. Теперь надо подобрать во вторых скобках числа так, чтобы вычитаемое равнялось 32. Сделать это реально, если мы возьмем числа 3, 4 и 9.
Задание под буквой а) сделано.
Переходим к букве б).
Формула для нахождения разности рейтингов у нас есть. Вот она:
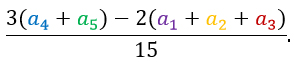
Т.к. это дробь, то она может быть правильной и неправильной.
Возьмем на пробу золотую середину – приравняем дробь к 1. Единицу мы получим лишь в том случае, если числитель дроби будет равен 15.
Не буду расписывать все мои пробы получения этого значения, сразу сделаю, как надо :)
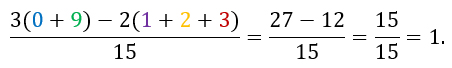
Есть, кстати еще, как минимум один вариант получения 1.
Но интересно, возможно ли получить число больше, чем 1?
Оказывается, что да.
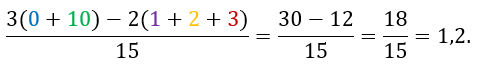
Ответ: а) да, если а1 = 4, а2 = 3, а3 = 9, а4 = 1, а5 = 10;
б) 1,2, если а1 = 1, а2 = 2, а3 = 3, а4 = 0, а5 = 10.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.