Написать уравнение касательной к параболе y=4x²-8, параллельной прямой, проходящей через точки (2; 3) и (7; 13). Сделать чертеж.

Запишем общее уравнение прямой, проходящей через 2 точки:

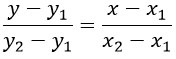
Пусть точка А имеет координаты (2; 3), а точка В - координаты (7; 13), тогда уравнение прямой, проходящей через точки А и В будет иметь вид

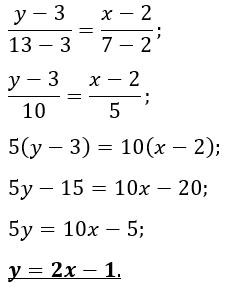
Выпишем общее уравнение касательной:

где a – абсцисса точки касания; 

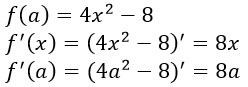
Если в уравнениях прямых y=k₁x+b₁ и y=k₂x+b₂ k₁=k₂, то прямые параллельны, следовательно

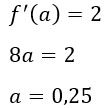
Найдем f(a).

Выведем уравнение касательной:

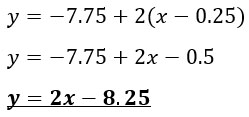
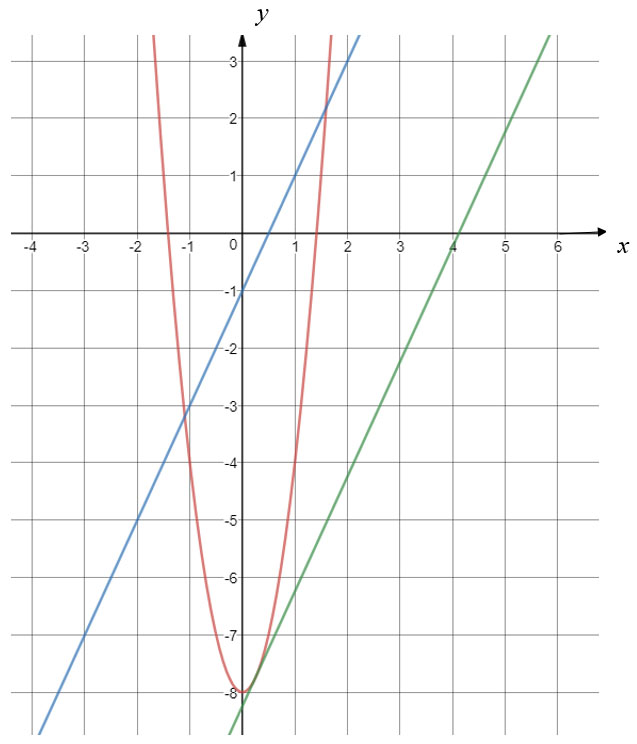
Начертим график.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.