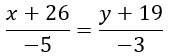Найдите проекцию точки A (10,-11) на прямую a, заданную уравнением (x+26)/(-5)=(y+19)/(-3). В ответе укажите сумму координат.

1 способ.

Шаг 1.  Записываем уравнение прямой b, которая проходит через точку А (10,-11) и перпендикулярна прямой a:

 - направляющий вектор прямой a. Т.к. a⊥b, то координаты вектора b являются координатами нормального вектора прямой a, т.е. .

Уравнение прямой b, проходящей через А (10,-11) и имеющей нормальный вектор , записывается в виде:

-5(x-10)-3(y-(-11))=0; 

-5x+50-3y-33=0; 

5x+3y-17=0 -уравнение прямой b.

Шаг 2. Найдем координаты проекции точки А на прямую a как координаты точки пересечения прямых a и b. Для этого решается система уравнений:

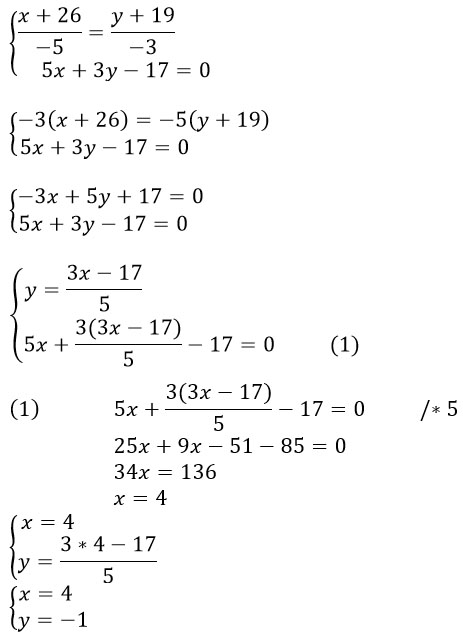
Проекция точки имеет координаты (4; -1).

Теперь найдем сумму координат: 4+(-1)=3

Ответ: 3.

2 способ.

Выразим y из :

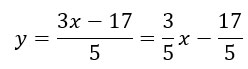
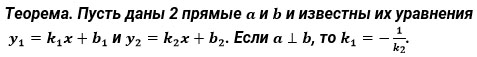
Т.е. если уравнение прямой a имеет вид

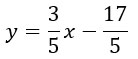
то уравнение прямой b будет выглядеть так:

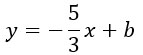
Подставим координаты точки А (10,-11) в уравнение прямой b:

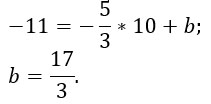
Приравняем уравнения:

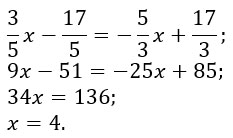
В любое уравнение подставляем x=4 и находим y.

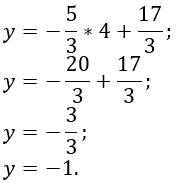
Проекция точки имеет координаты (4; -1).

Теперь найдем сумму координат: 4+(-1)=3

Ответ: 3.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.