Теоремы сложения вероятностей событий. Следствие из теорем сложения.

Теорема сложения несовместных событий.

Вероятность суммы двух несовместных событий равняется сумме вероятностей этих событий.

AB = V; P(A + B)=P(A) + P(B)

Доказательство (для схемы случаев). Пусть А и В – исходы n испытаний, которые сводятся к схеме случаев. Предположим, что событию А благоприятствуют m случаев, событию В – k случаев. Тогда вероятности событий А, B: 

P(A) = m/n  , P(B) = k/n

P(A) + P(B) = m/n + k/n = (m + k) / n (1)

P(A + B) = (m + k) / n (2)

(1) = (2) (по свойству транзитивности), значит P(A + B) = P(A) + P(B)

Следствия из теоремы.

1) Методом математической индукции можно обобщить для любого числа слагаемых:

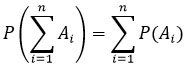
2) Сумма вероятностей двух противоположных событий равна 1:

P

3) Вероятность суммы событий, составляющих полную группу равна 1.

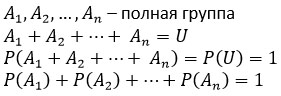
Теорема сложения для совместных событий.

Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

P(A + B) = P(A) + P(B) - P(AB)

Доказательство. Пусть события А и В – совместны. Тогда событие

События AB и несовместны, т.к.

Событие

События AB и несовместны, т.к.

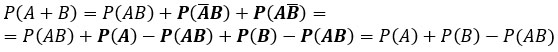
Обобщенная теорема сложения.

Вероятность появления хотя бы одного из данных событий равна разности между единицей и произведением вероятностей противоположных событий.

Доказательство. Пусть даны A₁, A₂, … , A_n.

Событие А – появление хотя бы одного из А_i (i = 1, … , n).

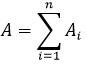
Рассмотрим событие B – ни одно из A_i не появляется:

События А и В противоположные ⇒ P(A) + P(B) = 1

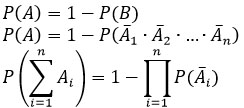
Если события A₁, A₂, … , A_n равновозможные, т.е. P(A₁) = P(A₂) = ⋯ = P(A_n) = p , тогда 

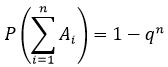
При подготовке к экзамену ориентируйтесь на лекции преподавателя!

О любой неточности прошу сообщить мне.

С уважением, Васильева Анна.