Методы решения уравнений, содержащих дроби

В этой статье я расскажу методики решения рациональных уравнений, содержащих дроби.

Что такое рациональное уравнение? Это уравнение, которое содержит в себе такие действия как сложение, вычитание, умножение, деление, возведение в степень с целым показателем. Извлечение корня - это недопустимое действие для рационального уравнения. Корень делает уравнение иррациональным, как, собственно, и дробный показатель степени.

В свою очередь рациональные уравнения делятся на два вида: целые рациональные и дробные рациональные.

К целым рациональным уравнениям относятся линейные и квадратные уравнения. Рассмотрим пример:

Это уравнение является...попробуешь угадать?...линейным. Его можно запросто увидеть, если деление на 2 и на 6 заменить умножением на 1/2 и 1/6 соответственно. Но оно все-таки содержит в себе знаменатель, поэтому мы его и рассматриваем в данной статье.

К дробным рациональным уравнениям относятся уравнения, которые содержат икс в знаменателе. Например, это уравнение дробное рациональное:

Методика решения приведенных примеров, в принципе, одинакова. Разница состоит в том, что в дробных рациональных уравнениях знаменатель не должен равняться нулю, поэтому при их решении оговаривают ограничения для икса. По-научному говорят, что находят область допустимых значений (ОДЗ).

Но давайте начнем с простого.

Целое рациональное уравнение.

Сначала решим целое рациональное уравнение.

Если ты в уравнении видишь дроби, то надо от них избавится, ведь уравнение без дробей решается намного приятнее)

В этом уравнении находим общий знаменатель. Он равен 6. Это значит, что обе части уравнения надо умножить на 6 (одинокий икс тоже).

Обычно этот шаг пропускают и переходят к следующему, но я его все равно распишу:

Числители и знаменатели сокращаются и получается элементарное уравнение:

Приводим подобные слагаемые:

Чтобы найди икс надо -10 разделить на 10 (произведение делим на известный множитель). Получаем ответ:

Готово!

Дробное рациональное уравнение.

Теперь решим дробное рациональное уравнение.

Я уже писала о том, что в дробных рациональных уравнениях знаменатели не должны равняться нулю. Знаменатель второй дроби нас устраивает, ведь 3 не равно 0) А вот знаменатель первой дроби требует от нас, чтобы мы нашли ОДЗ.

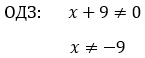
А дальше по накатанной: надо обе части уравнения умножить на общий знаменатель. Общим знаменателем будет выражение 3(х + 9).

Снова распишу подробно, но если ты шаришь, то следующую запись можешь не писать.

В первой дроби сокращаем (х + 9), а во второй - тройки. Получаем такое уравнение:

Здесь можно раскрыть скобки, потом перенести известные в одну сторону, а неизвестные - в другую... Но делать я этого не стану, а просто обе части уравнения разделю на -2. А еще поменяю местами левую и правую части уравнения, чтобы привести его к привычному виду.

Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое, т.е. из -9 вычесть 9.

Ответ таков:

Сравниваем с ОДЗ... Всё отлично. Корень уравнения подходит.

Альтернативный метод решения уравнения с дробями.

Но нельзя пройти мимо другого метода решения данного уравнения: с помощью пропорции. Помнишь, как она раскрывается? Правильно, крест-накрест. И не надо искать общий знаменатель)

Перемножаем....и о чудо! Получаем уравнение, которое мы уже решали!

Дальнейшее решение расписывать не буду, оно есть выше.

Такой способ решения уравнений хорош, когда в уравнении имеются две дроби.

В завершении решу еще одно уравнение предложенными выше способами.

Только ты решаешь какой способ выбрать.

Твой персональный препод Васильева Анна)