Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

Степень - это произведение одинаковых множителей, состоящая из основания и показателя. Наглядно это можно рассмотреть на рисунке ниже.

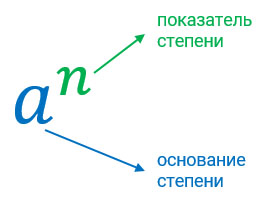
Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

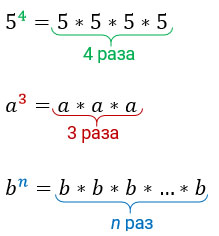
Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

1. Любое число в первой степени равно самому себе: a¹ = a.

Сразу рассмотрим примеры.

2¹ = 2;

(-10)¹ = -10;

0¹ = 0.

2. Любое число в нулевой степени равно 1: а⁰ = 1.

Примеры:

2⁰ = 1;

(-3)⁰ = 1;

0⁰ = 1.

3. Единица в любой степени равна 1: 1ⁿ = 1.

4. При умножении степеней с одинаковыми основаниями показатели складываются: aⁿ · a^m = a^{n + m}.

Почему так?

Это свойство легко доказать на числовом примере.

2³ · 2² = 2 · 2 · 2 · 2 · 2 = 2⁵.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3⁴ · 3⁹ · 3¹⁵ = 3^{4 + 9 + 15} = 3²⁸;

(-2)³ · (-2)⁴ = (-2)^{3 + 4} = (-2)⁷.

5. При делении степеней с одинаковыми основаниями показатели вычитаются: aⁿ : a^m = a^{n - m} (a ≠ 0).

Доказывается эта формула тоже очень просто с помощью числового примера: три четверки из числителя сокращаем с тремя четверками из знаменателя и остаются две четверки в числителе, т.е. 4².

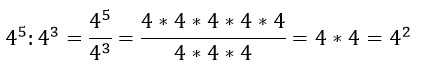
Еще парочка примеров:

15¹⁰ : 15³ : 15⁵ = 15^{10 - 3 - 5} = 10²;

(-3)¹¹ : (-3)⁵ = (-3)^{11 - 5} = (-3)⁶.

6. При возведении степени в степень показатели умножаются: (аⁿ)^m = a^nm.

Примеры:

(2²)³ = 2^{2 · 3} = 2⁶;

(5³)¹⁰ = 5^{3 · 10} = 5³⁰.

7. При возведении произведения в степень каждый множитель возводится в эту степень: (ab)ⁿ = aⁿbⁿ.

Примеры:

(5 · 4)² = 5² · 4²;

(2 · 3  · 4 · 5)^а = 2^а · 3^а · 4^а ·5^а.

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.

Пример:

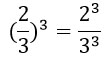
9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле (а > 0, n ≥ 2).

Пример:

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: (a ≠ 0).

Это же правило работает и для дробей:  (a ≠ 0, b ≠ 0).

Примеры:

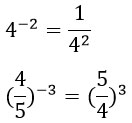
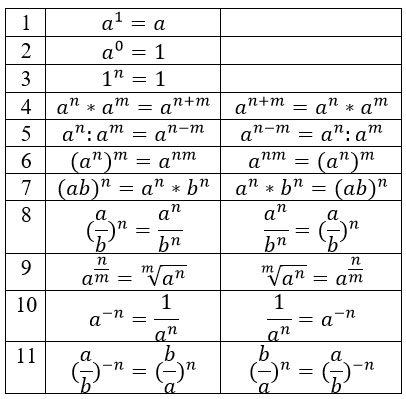
Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

Напоследок, разберем пример, который может встретиться во второй части ОГЭ по математике. Он, конечно, не охватывает сразу все формулы - только несколько из них.

Нам нужно сократить такую дробь:

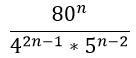
Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

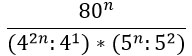
Получившиеся частные в знаменателе запишем в виде дробей.

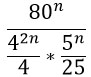
Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх :)

К тому же здесь можно воспользоваться свойством 6 из второго столбика и 4²ⁿ превратится в 16ⁿ.

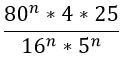
Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

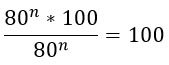
Успехов в учебе!

С уважением, Васильева Анна.