Синус, косинус, тангенс и котангенс
Острые углы в прямоугольном треугольнике.
В геометрии определения синуса, косинуса, тангенса и котангенса мы изучаем на примере острых углов в прямоугольном треугольнике.
Вот и они:

Возьмем прямоугольный треугольник АВС и распишем для него формулы для нахождения синуса, косинуса, тангенса и котангенса острых углов α и β.
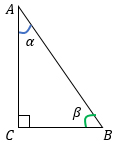
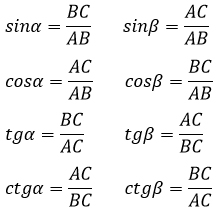
Острые углы прямоугольного треугольника обладают очень интересными сверхспособностями, которые могут пригодится при решении геометрических задач.
Во-первых, их сумма равна 90°.
Во-вторых, верны будут следующие равенства (доказать их верность очень легко - смотри предыдущие 8 формул):
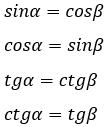
Смежные углы.
Теперь немного отстранимся от прямоугольных треугольников. Есть еще очень клевые формулы, но они подходят для смежных углов.
Пусть даны смежные углы α и β (напомню, что сумма смежных углов равна 180°).
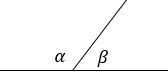
Для них будут верны следующие равенства (доказываются через формулы приведения, т.к. α = 180° - β):
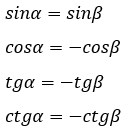
Формулы приведения.
| Функции | Углы | ||||||||
| -α | 90°-α | 90°+α | 180°-α | 180°+α | 270°-α | 270°+α | 360°-α | 360°+α | |
| sin | -sinα | +cosα | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα |
| cos | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα | +cosα | +cosα |
| tg | -tgα | +ctgα | -ctgα | -tgα | +tgα | +ctgα | -ctgα | -tgα | +tgα |
| ctg | -ctgα | +tgα | -tgα | -ctgα | +ctgα | +tgα | -tgα | -ctgα | +ctgα |
Таблица значений тригонометрических функций для "прекрасных" углов.
| α | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tgα | 0 | √3/3 | 1 | √3 | - | 0 | - | 0 |
| ctgα | - | √3 | 1 | √3/3 | 0 | - | 0 | - |
Осталось это всё запомнить и научиться применять на практике)
Вообще, достаточно запомнить информацию только про синусы и косинусы, а уже через них выводить значения тангенса и котангенса.
Еще рекомендую к прочтению статью про тригонометрические тождества.
Успехов в подготовке!
С уважением, Васильева Анна.

