Обратная пропорциональность и её график

Рассмотрим функцию, которая задается формулой 

.

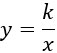Такая функция называется обратной пропорциональностью, причем x ≠ 0 (т.к. на 0 делить нельзя). Число k также отлично от 0 (в противном случае функция перестанет являться обратной пропорциональностью). Её графиком является гипербола, состоящая из двух ветвей. Ты сможешь увидеть ее ниже.

Перед разбором тренировочных экзаменационных заданий очень хочется вспомнить, что конкретно влияет на расположение и вид графика.

Напомню, что координатная плоскость делится на 4 координатных четверти. У каждой четверти есть свой порядковый номер (см. рисунок).

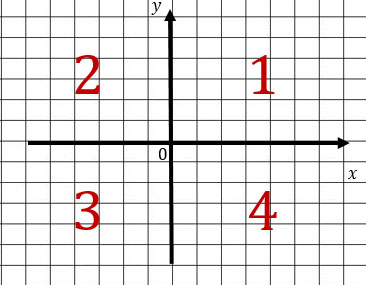
Так вот к чему я это?

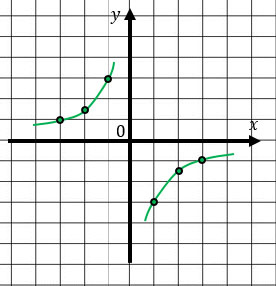
Если k > 0, то ветви гиперболы располагаются в 1 и 3 четвертях.

Если k < 0, то ветви гиперболы располагаются во 2 и 4 четвертях.

Убедимся в этом) Построим два графика.

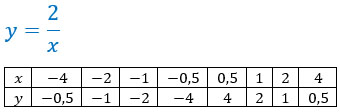
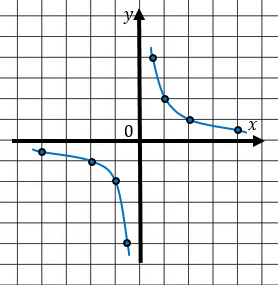
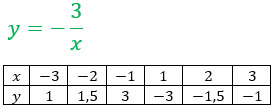
Чем больше точек ты запишешь, тем точнее получится график.

В обоих случаях ветви гиперболы никогда не пересекут оси Ох и Оу, т.к. ни х, ни у нулю равняться не могут. Это значит, что оси являются для графика асимптотами - ветви гиперболы бесконечно стремятся к ним, но никогда их не пересекают.

Но не всегда оси будут асимптотами.

Например, в следующей функции асимптотами будут являться прямые х = 2 и у = 1.

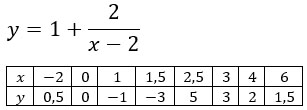
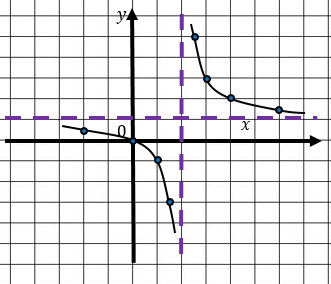
Практикум по гиперболам.

Оказывается, что на сайте ФИПИ все задания чисто с гиперболами однотипные, поэтому разберу только два задания, похожих друг на друга (почему они оси не прорисовывают не пойму).

Задание 1. Установите соответствие между графиками и их функциями.

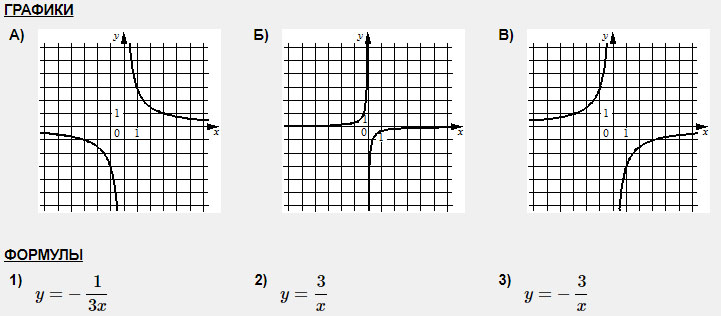
Из общей массы выделяется график Б, т.к. ветви этой гиперболы находятся очень близко к началу координат. А из формул выделяется формула 1, т.к. в ее знаменателе икс умножен на 3. Вывод: график Б и формула 1 созданы друг для друга!

Далее, ветви графика А расположены в 1 и 3 четвертях плоскости, значит коэффициент k положительный. К А подходит формула 2.

И остались график В и формула 3.

Всё)

Задание 2. Установите соответствие между функциями и их графиками.

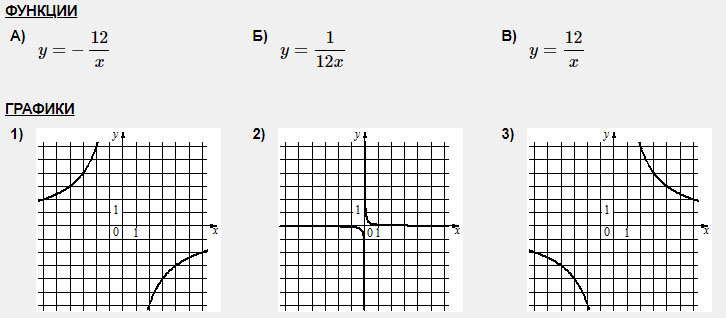
Аналогично предыдущему заданию.

Б-2

А-1

В-3