Линейные неравенства

Линейные неравенства представляют собой неравенства вида ax + b < 0, ax + b > 0, ax + b ≥ 0, ax + b ≤ 0, где а и b - некоторые число и а ≠ 0.

Они решаются точно также, как и линейные уравнения, но есть, конечно, существенные отличия: в неравенствах ответом является какой-то числовой промежуток.

А еще при делении обеих частей на отрицательное число знак неравенства меняется.

Чтобы решить линейное неравенство надо с помощью различных преобразований привести его к такому виду, чтобы переменная х осталась в левой части неравенства; далее, с помощью числовой прямой, нужно определить все значения х, которые удовлетворяют неравенству и записать их в виде числовых промежутков.

Обычно, все эти названия мы не используем, а просто говорим, что икс принадлежит промежутку от а до b или от а до плюс бесконечности, включая а, и т.д.

Если число не принадлежит промежутку, то берем его в круглую скобку (знаки > и <), а если принадлежит, то в квадратную (знаки ≥ и ≤). От таких нюансов зависит правильность ответа.

Давайте посмотрим, какие задания с линейными неравенствами нам предлагает сайт ФИПИ для подготовки к ОГЭ по математике.

Задание 1.

Перенесем известные в правую часть неравенства, а неизвестные - в левую (с противоположными знаками!):

- х - х ≥ 3 - 6.

Приведем подобные слагаемые:

-2х ≥ -3.

Разделим обе части неравенства на -2. Т.к. делим на отрицательное число, то меняем знак неравенства на ≤:

х ≤ 1,5.

На числовой прямой отмечаем число 1,5 и показываем, где будут находится числа, которые меньше или равны 1,5.

Решением неравенства будет промежуток от минус бесконечности до 1,5 включительно.

Подходит вариант ответа под цифрой 1.

Ответ: 1.

Задание 2.

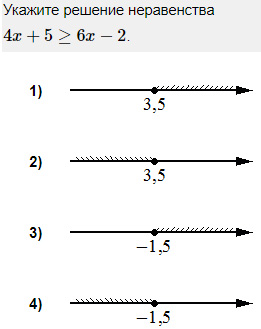
Снова переносим известные в одну сторону, а неизвестные - в другую (с противоположными знаками!):

4х - 6х ≥ -2 -5.

Приводим подобные:

-2х ≥ -7.

Делим обе части неравенства на -2 и меняем знак неравенства, т.к. -2 - отрицательное число:

х ≤ 3,5.

Решение такого неравенства изображено на числовой прямой под номером 2.

Ответ: 2.

Задание 3.

Первым делом раскроем скобки:

3х - 2х + 10 ≤ -6.

Перенесем известные в одну сторону, а неизвестные в другую. Сразу приведем подобные слагаемые:

х ≤ -16.

На числовой прямой отметим число -16 и все числа, которые меньше -16.

Такому графическому изображению соответствует третий вариант ответа.

Ответ: 3.

Задание 4.

В системах страшного ничего нет: решаем как обычно, просто делаем это с двумя неравенствами одновременно.

Переносим числа в правую часть неравенства с противоположными знаками и сразу приводим подобные слагаемые. Исходная система примет вид:

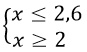
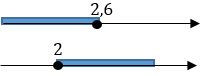
Начертим две числовые прямые. На первой прямой отметим решения для первого неравенства, а на второй - решения для второго. Обрати внимание, что отмеченные на этих прямых числа должны соответствовать своей логике: меньшее число должно быть левее, чем большее.

Теперь нужно выбрать решение, подходящее для обоих неравенств одновременно (Есть такие понятия "объединение" и "пересечение" промежутков. При решении систем нам нужно именно "пересечение".). Я выделю его оранжевым цветом.

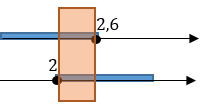
Теперь возвращаемся к вариантам ответа. Получившееся у нас графическое изображение соответствует первому числовому промежутку.

Ответ: 1.

Задание 5.

Переносим известные в одну сторону, неизвестные - в другую. Сразу приводим подобные слагаемые.

Обе части первого неравенства делим на 4, а обе части второго делим на -3. При этом знак второго неравенства меняется на <.

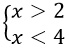
Чертим две числовые прямые. На первой отмечаем все иксы, которые больше 2, а на второй - все иксы, которые меньше 4.

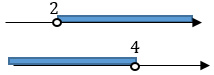
Выбираем промежуток, который удовлетворяет обоим неравенствам: от 2 до 4.

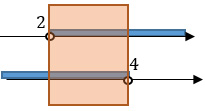
Возвращаемся к вариантам ответа: промежуток под номером 4 является решением системы неравенств.

Ответ: 4.

Задание 6.

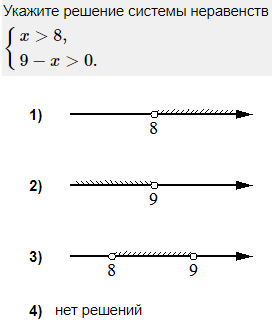
Первое неравенство уже готовенькое. Работаем только со вторым. Перенесем число 9 в правую часть с противоположным знаком.

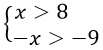
Разделим обе части второго неравенства на -1. При этом меняется знак неравенства.

По аналогии с предыдущим примером решением этой системы неравенств является промежуток от 8 до 9. Он изображен в 3 варианте ответа.

Ответ: 3.

В этой статье, написанной специально для сдающих ОГЭ, разобраны самые простые виды линейных неравенств. Как видишь, экзамен достаточно прост)

Васильева Анна, твой персональный преподаватель.