Кредит. Аннуитетный и дифференцированный платежи.
Кредит - это финансовая сделка, в результате которой кредитор (как правило, банк) предоставляет деньги заемщику на определенный срок. Естественно, что за пользование этими деньгами заемщик должен будет отдать некоторую сумму сверх той, что он взял в кредит, другими словами, выплатить проценты.
Рассмотрим ситуацию.
Гражданин взял в банке 1000 рублей под 30% годовых.
Что это значит? Это значит, что через год гражданин должен будет вернуть 1000 рублей плюс 30% от 1000.
Узнаем, сколько рублей гражданин выплатит банку через год:
1000 + 0,3 · 1000 = 1000 + 300 = 1300 (проценты обязательно переводим в дроби: 30% = 0,3).
Обобщим этот случай.
Пусть гражданин взял в кредит S рублей под а% годовых. Сколько денег он отдаст банку через год? Получаем такую запись:
![]()
Немного преобразуем ее, вынеся общий множитель S за скобку:
![]()
Получилось, что исходная сумма S увеличилась в (![]() ) раз.
) раз.
Назовем число (![]() ) полезным коэффициентом и обозначим буквой m.
) полезным коэффициентом и обозначим буквой m.
Итак, перед тем, как переходить к решению задач, введем систему обозначений:
S - сумма кредита;
а - проценты;
m - полезный коэффициент (![]() );
);
х - выплаты по кредиту;
n - количество лет, на которое берут кредит.
Чуть ниже мы разберем два типа задач: на аннуитетный платеж и на дифференцированный.
Аннуитетный платеж подразумевает под собой равные выплаты в течении всего времени погашения кредита, но при этом банк до внесения платежа начисляет процент на оставшуюся часть долга.
Дифференцированный платеж подразумевает уменьшение суммы долга равномерно, на одну и ту же величину; причем выплаты каждый раз разные. Это значит, что если кредит взяли на n лет на сумму S, то ежегодно сумма долга уменьшается на S/n по сравнению с долгом на начало года.
Возьмем две задачи, похожие по структуре, и на них прочувствуем разницу между аннуитетным и дифференцированным платежами.
Задача 1.
В июле 2020 года планируется взять кредит в банке на сумму 545 000 рублей. Условия его возврата таковы: - каждый январь долг увеличивается на 40% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить одним платежом часть долга. Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года)?
В условии прописано, что кредит выплачивают равными платежами; очевидно, что это аннуитентный платеж.
Дано:
S = 545 000
a = 40
n = 3
m = 1 + 40/100 = 1,4.
Найти: 3х (х - это одна из трех выплат, которыми полностью погашают трехлетний кредит).
Решение:
Выведем формулу, по которой будет решаться наша задача.
1 год. Мы взяли кредит на сумму S. Эта сумма увеличилась в m раз (полезный коэффициент, читай про него выше) и мы выплатили некоторую сумму х. Остаток долга на конец первого года стал равен
Sm - х.
2 год. Остаток долга снова увеличился в m раз и мы произвели выплату, равную х. Теперь на конец второго года остаток долга равен
(Sm - x)m - х = Sm2 - xm - x.
3 год. Опять остаток увеличился в m раз, мы выплачиваем х рублей и прощаемся с кредитом:
(Sm2 - xm - x)m - x = Sm3 - xm2 - xm - x = 0.
Выразим и найдем х.
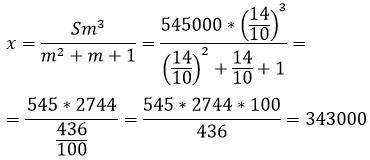
Это мы нашли одну выплату, а нам надо 3.
343 000 · 3 = 1 029 000 рублей мы выплатим за 3 года, чтобы погасить кредит полностью.
Ответ: 1 029 000 рублей.
Эта задача, кстати, у меня решена еще и старым дедовским способом (без формул и полезных коэффициентов). Посмотреть ее можно здесь.
Задача 2.
15 января планируется взять кредит на 5 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше (Этот набор слов сразу говорит о том, что задача на дифференцированный платеж. Предупрежден - значит вооружен!) долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Дано:
S (некоторая сумма)
a = 5
n = 5
m = 1 + 5/100 = 1,05
x1 + x2 + ... + x5 - общая сумма денег, потраченная на погашение кредита
Найти: сколько % от S составляет общая сумма денег.
Решение.
1 месяц. Та сумма, которую мы взяли увеличивается в m раз и происходит первая выплата х1. Получается, что долг становится равен Sm - x1. Прям как при аннуитентном платеже.
НО! Наш долг каждый месяц на одну и ту же сумму меньше долга предыдущего месяца. Это значит, что каждый месяц долг уменьшается на 1/5 часть исходной суммы S. (1/5 потому, что кредит взяли на 5 месяцев, т.е. сумму кредита поделили на 5 равных частей).
Это можно записать как ![]() .
.
Т.е. получается, что
![]() .
.
2 месяц. Остаток долга 4S/5 увеличивается в m раз и производится вторая выплата х2. Действуем аналогично первому месяцу.
![]() .
.
Все то же самое происходит в третьем и четвертом месяце. Если вы заметили какую-нибудь закономерность, то это просто супер! Эти месяцы можно не расписывать. Вообще нас интересуют первый и последний месяцы.
5 месяц - месяц, в котором мы выплачиваем весь кредит.
![]()
Т.к. долги последующих месяцев на одну и ту же сумму меньше долгов предыдущих, то мы с уверенностью можем сказать, что сумма долгов уменьшается в арифметической прогрессии, следовательно, и выплаты х1, ..., х5 тоже.
Найдем общую сумму денег, потраченную на погашение кредита по формуле суммы первых n членов арифметической прогрессии.
![]()
Выразим x1 и x5.
![]()
![]()
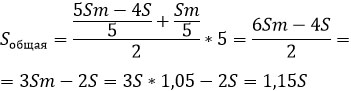
Далее составим пропорцию и найдем, сколько процентов составляет общая сумма денег.
S - 100%
1,15S - y%
![]()
Ответ: 115%.
Очень надеюсь, что после разбора данных задач вам легче станет ориентироваться в задачах на кредиты. В принципе, они не очень сложные, если в них как следует разобраться. А успешность решения напрямую зависит от практики. Пробуйте решать задачи самостоятельно и у вас обязательно все получится!
Успешной сдачи экзаменов!
С уважением, Васильева Анна.

