Наибольшее и наименьшее значение функции. Точки максимума и минимума.
Разбираться в теории лучше всего на практическом примере, поэтому возьмем для рассмотрения простенькую функцию
y = -x3 + 3x2 + 9x - 29 на отрезке [-1; 4].
Исследование этой функции начинается одинаково как для нахождения наибольшего и наименьшего значения функции, так и для нахождения максимума и минимума.
Шаг 1. Находим первую производную.
y' = -3x2 + 6x + 9.
Шаг 2. Найдем критические точки, в которых производная либо равна 0, либо не существует. Если проще, то приравняем производную к 0 и найдем корни получившегося уравнения.
-3x2 + 6x + 9 = 0 /(:-3)
x2 - 2x - 3 = 0;
По теореме Виета
х1 = 3; х2 = -1.
Оба корня принадлежат отрезку.
На этом общий алгоритм заканчивается.
Находим наибольшее/наименьшее значение и максимум/минимум функции по отдельности.
| Наибольшее и наименьшее значение функции | Точки максимума и минимума |
|
Подставим найденные критические точки и концы отрезка в уравнение функции. y(3) = -33 + 3*32 + 9*3 - 29 = -2; y(-1) = -(-1)3 + 3*(-1)2 + 9*(-1) - 29 = -16; y(4) = -43 + 3*42 + 9*4 - 29 = -9. Выбираем наибольшее и наименьшее значения функции. Наибольшее: -2. Наименьшее: -16 |
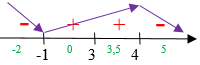
На числовой прямой отметим критические точки и концы отрезка.
Возьмем произвольные числа из получившихся промежутков и подставим в уравнение производной функции. Определим знаки промежутков и расставим стрелочки: если промежуток положительный, то стрелочка пойдет вверх, если отрицательный, то вниз.
По рисунку видно, что точка максимума равна 4, а точка минимума равна -1. |
Успешной сдачи экзаменов!
С уважением, Васильева Анна.