Действия с десятичными дробями

Изначально существовали только обыкновенные дроби, но со временем появилась более удобная запись дробей со знаменателями 10, 100, 1000 и т.д.

Такая запись состояла из целой части и числителя, разделенные между собой запятой; при этом количество знаков после нее должно было быть равно количеству нулей в знаменателе.

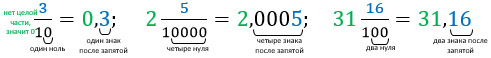
Но любую другую дробь тоже можно перевести в десятичную. Для этого надо в столбик разделить числитель на знаменатель. Тут возможны два варианта развития событий: дробь может быть конечной или бесконечной.

Чтобы смешанное число перевести в десятичную дробь не надо переводить его в неправильную. Достаточно лишь разделить числитель на знаменатель, т.к. целая часть остается без изменений.

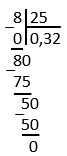
Бесконечная десятичная дробь бывает периодической и непериодической. 

Обыкновенную дробь можно представить только в бесконечной периодической, если она не конечная, конечно же)

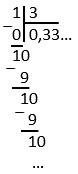
Период у дроби необязательно начинается сразу после запятой.

Может быть и такое: 2,721541541541... = 2,72(154).

Сложение и вычитание десятичных дробей.

Чтобы в столбик сложить/вычесть десятичные дроби надо записать их так, чтобы запятая была под запятой, уровнять количество знаков после запятых, сложить/вычесть их, не обращая внимания на запятую, а затем поставить запятую под запятыми (вот это я лихо написала!).

На примерах будет совсем всё понятно)

1) Сложим сначала целое число с десятичной дробью. Целое число тоже представимо в виде десятичной дроби - достаточно поставить после него запятую и дописать столько нулей, сколько необходимо для сложения и вычитания.

4 + 3,25 = ?

А теперь тот же пример, только с минусом:

2) Сложим/вычтем две десятичные, у которых количество знаков после запятой одинаковое.

3) А теперь примеры с разным количеством знаков после запятой в дробях. Возьмем дроби 6,2 и 3,064.

Умножение десятичных дробей.

Чтобы в столбик умножить десятичные дроби надо записать их как при умножении натуральных чисел, не обращая внимания на запятые; умножить; в ответе с конца отсчитать столько знаков после запятой, сколько их стоит после запятой в обеих дробях.

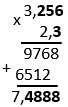
При умножении десятичной дроби на число действует это же правило.

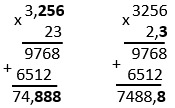
Чтобы каждый раз не умножать десятичную дробь на 10, 100, 1000 и т.д. достаточно запомнить, что при умножении на эти числа запятая у дроби перемещается вправо на столько знаков, сколько нулей стоит в числе.

Деление десятичных дробей.

Сначала разберем деление десятичной дроби на натуральное число. Деление в столбик происходит как обычно: делим не обращая внимания на запятую, НО, как только мы снесли вниз первую цифру из дробной части, надо в частное поставить запятую.

Например, при делении 4,92 на 4 запятая ставится в частное при снесении цифры 9. Другими словами, как только мы заканчиваем делить целую часть, сразу ставим запятую.

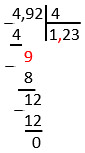
Теперь рассмотрим деление на десятичную дробь.

На десятичную дробь делить просто так нельзя - нужно сначала перенести запятые в обоих числах на столько цифр, сколько их после запятой в делителе. Делитель - это второе число)

Вообще, этот перенос запятых осуществляется умножением обоих чисел на 10, 100, 1000 и т.д.

Попробуем разделить две дроби на примере: 14,1289 : 6,143.

В делителе три знака после запятой. Значит, оба числа надо умножить на 1000 или просто перенести запятые на три знака вправо.

14,1289 : 6,143 = 14128,9 : 6143 = ...

При делении опять, как только снесли первую цифру из дробной части, сразу поставили запятую в частное.

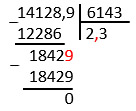
14,1289 : 6,143 = 2,3.

Чтобы каждый раз не делить десятичную дробь на числа 10, 100, 1000 и т.д. достаточно запомнить, что при делении на эти числа запятая у дроби перемещается влево на столько знаков, сколько нулей стоит в числе.

Округление.

Очень часто в экзаменационных задачах мы видим "округлите до десятых" или "округлите до целого"... Что это вообще значит?

Округление - это замена какого-то числа ближайшим к нему числом, причем, если число округляют до какого-нибудь разряда, то все следующие за ним цифры до запятой становятся нулями, а цифры после запятой отбрасываются.

Если первая замененная нулем или отброшенная цифра  была равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменений. В остальных случаях (5, 6, 7, 8, 9) ее увеличивают на 1.

Возьмем число 9814,3516 и округли его до тысячных, сотых, десятых, единиц, десятков, сотен, единиц тысяч (разряд округления буду подчеркивать).

1) До тысячных: 9814,3516 ≈ 9814,352 (после единицы стоит цифра 6, значит надо прибавить единицу к разряду тысячных, а шестерка обращается в 0 и отбрасывается).

2) До сотых: 9814,3516 ≈ 9814,35 (после пятерки стоит 1, значит разряд сотых остается без изменений; все остальное отбрасыватся).

3) До десятых: 9814,3516 ≈ 9814,4 (после тройки стоит 5, значит к разряду десятых прибавляем 1; остальное отбрасываем).

4) До единиц: 9814,3516 ≈ 9814 (после четверки стоит 3; разряд не меняем, остальное отбрасываем).

5) До десятков: 9814,3516 ≈ 9810 (после единицы стоит 4 - разряд не меняется; после разряда десятков цифры до запятой обращаются в нули (в данном случае это только одна цифра), после запятой - отбрасываются).

6) До сотен: 9814,3516 ≈ 9814,352 (после 8 стоит 1, разряд не меняется, цифры до запятой обращаются в нули, после запятой - отбрасываются).

7) До единиц тысяч: 9814,3516 ≈ 10000 (после девятки стоит 8, значит к разряду единиц тысяч прибавляется 1, цифры до запятой обращаются в 0, после запятой - отбрасываеются).

Ну что, скил прокачан? Если да, то супер)

Успехов в учебе!