Арифметический квадратный корень и его свойства
Арифметическим квадратным корнем из числа a называют такое неотрицательное число b (b ≥ 0), вторая степень которого равна a.
Запишем это определение на математическом языке:
![]()
Убедимся в правильности данной записи на примере. Пусть а = 16, b = 4, тогда
![]()
Всё верно: если 4 в квадрате равно 16, значит корень из 16 равен 4.
Извлечем парочку корней:
√0 = 0;
√1 = 1;
√4 = 2;
√256 = 16 и т.д.
Обратите внимание, что подкоренное выражение неотрицательно! Извлечение корней из отрицательных чисел - это уже совсем другая история и в школьной математике не рассматривается.
Свойства арифметического квадратного корня (далее корень).
1. Корень произведения равен произведению корней (а ≥ 0, b ≥ 0).
![]()
Примеры:
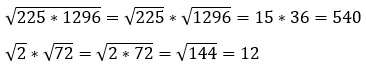
2. Корень частного равен частному корней (а ≥ 0, b > 0).
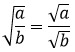
Примеры:
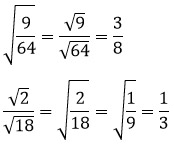
3. Корень в квадрате равен подкоренному выражению (а ≥ 0).
![]()
Примеры:
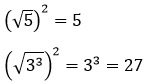
4. Корень из квадрата числа равен модулю этого числа (а - любое).
![]()
Примеры:
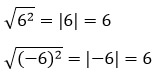
5. Корень из степени с основанием а и показателем n равен корню из числа а в степени n (а ≥ 0, n - натуральное).
![]()
Пример:
![]()
Свойство работает в обе стороны.
6. Квадратный корень числа в четной степени равен этому числу в степени, деленной на 2.
![]()
Пример:
![]()
Вынесение множителя за знак корня.
Рассмотрим вынесение множителя на примере: возьмем число √12.
Число 12 можно разложить на два множителя - 3 и 4; один из них извлекается. Значит, из-под корня выносится двойка (корень из 4), а под корнем остается 3.
То же самое запишу на математическом языке:
![]()
Возьмем число побольше: √845.
Очевидно, что подкоренное выражение делится на 5, т.е. один из множителей равен 5, тогда второй равен 169 (169 · 5 = 845). Корень из 169 извлекается, значит из-под корня выносится множитель 13, а под корнем остается 5.
![]()
И возьмем число √28800.
Оно делится на 100, значит его можно представить в виде произведения чисел 100 и 288. Но 288 тоже можно разложить на произведение чисел 144 и 2. Это значит, что под корнем остается число 2, а выносятся сразу два множителя - 10 и 12, которые в дальнейшем нужно перемножить.
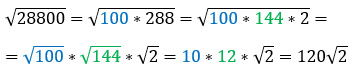
Еще есть второй способ - он короче. Здесь важно заметить, что 28800 - это произведение 14400 и 2. Результат не меняется.
![]()
Внесение множителя под знак корня.
Как в случае с вынесением рассмотрим внесение множителя под знак корня на примерах.
Возьмем число 2√3. Для внесения необходимо множитель перед корнем возвести в квадрат и умножить на подкоренное выражение. Получившееся число записываем под корнем.
![]()
Специально взяла пример из раздела "Вынесение множителя за знак корня" для того, чтобы вы убедились в правильности данного решения. Второй этап решения (произведение корней √22 и √3), кстати говоря, всегда пропускают.
Следующий пример: 5√7.
Пятерку возводим в квадрат и умножаем на 7. Результат записываем под знаком "корня".
![]()
Успехов в учебе!

