Окружность пересекает стороны АВ и ВС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. 1) Докажите, что треугольник АВС подобен треугольнику АРК. 2) Найдите длину отрезка КР, если АК=14, а сторона АС в 2 раза больше стороны ВС.

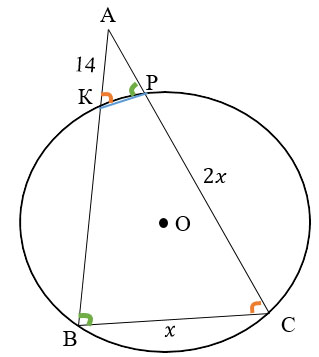
**Отрезок КР на чертеже виден плохо, но он там есть :)

Дано:

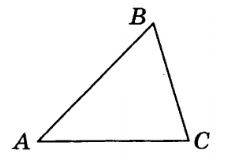
ΔАВС

окр. (О; ОВ)

АК=14

АС=2ВС

Доказать: ΔАВС ∼ ΔАРК.

Найти: КР.

Решение:

Пусть ВС=х, тогда АС=2х.

Рассмотрим треугольники АКР и АВС и докажем, что они подобны.

Т.к. четырехугольник КРСВ вписан в окружность, то сумма его противоположных углов равна 180°, т.е.

∠КВС+∠КРС=180°,

∠ВКР+∠РСВ=180°.

Сумма смежных углов равна 180°, значит

∠АКР+∠ВКР=180°,

∠АРК+∠КРС=180°.

Из этих четырех равенств следует, что ∠АКР=∠РСВ, ∠АРК=∠КВС. Добавляем сюда тот факт, что ∠А в треугольниках общий, а это значит, что ΔАКР∼ΔАВС по трем углам.

Что и требовалось доказать.

В подобных треугольниках стороны одного треугольника пропорциональны сходственным сторонам другого. Это значит, что

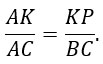
Подставляем все известные величины, получаем пропорцию, раскрываем ее крест накрест и решаем простейшее уравнение:

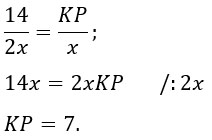
Ответ: 7.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.