На клетчатой бумаге с размером клетки 1 × 1 изображён равносторонний треугольник. Найдите: а) радиус описанной около него окружности; б) радиус вписанной в него окружности.

Небольшое лирическое отступление.

Точка пересечения серединных перпендикуляров в любом треугольнике является центром описанной окружности.

Точка пересечения биссектрис любого треугольника является центром вписанной в любой треугольник окружности.

Но в равностороннем треугольнике биссектрисы и серединные перпендикуляры совпадают, значит совпадают и центры вписанной и описанной окружностей.

В правильном треугольнике точка пересечения биссектрис (медиан или высот) делит их в отношении 2 к 1, начиная от вершины.

Это значит, что большая часть биссектрисы (медианы, высоты) является радиусом описанной окружности, а меньшая часть - радиусом вписанной окружности.

Осталось их найти.

Решение.

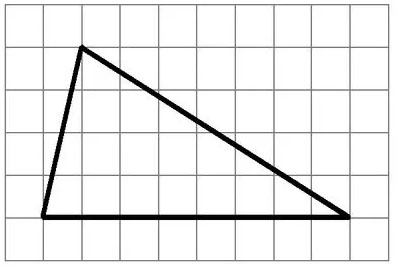
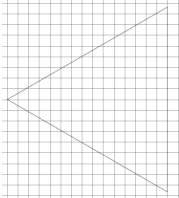
Сделаем доп. построение: прочертим медианы (высоту, биссектрису, называй, как хочешь).

Где-то на этом синем отрезке и находится общий центр описанной и вписанной окружностей, причем он делит отрезок в отношении 2 к 1.

Длина отрезка равна 15 клеткам.

Обозначим одну часть этого отрезка за k, тогда радиус описанной окружности будет равен 2k, соответственно радиус вписанной окружности будет равен просто k. Т.к. всего частей 15, то составим и решим уравнение:

2k + k = 15;

3k = 15;

k = 5 - длина одной части и длина радиуса вписанной окружности.

А радиус описанной окружности в два раза больше и равен 10.

Ответ: а) 10; б) 5.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.