Аксиоматическое построение теории вероятностей
Развитие естествознания в начале двадцатого века предъявило теории вероятностей новые ценностные требования. Нужно было дать систематическое, стройное определение основных понятий, сформулировать условия для них. Встала задача аксиоматического построения теории вероятностей. Впервые эта задача была поставлена и решена советским математиком Бернштейном в 1917 году. При этом он исходил из качественного сравнения случайных событий по их большей или меньшей вероятности. Свою точку зрения он высказал в работе «Опыт аксиоматического построения теории вероятностей». Затем был издан учебник. Другой подход изложил Колмогоров. В основу аксиоматики положено множество элементарных событий U. Далее рассматривается система F – подмножество U. Ее элементы называются случайными событиями. Системе F удовлетворяет:
1) в качестве элемента содержит множество U;
2) если А и В - случайные события, являются элементами системы F, то элементами f являются 
А+В – событие, элементами которого являются или элементы события А, или элементы события В, или элементы событий А и В.
А*В – событие, элементами которого являются элементы события А и элементы события В.
– противоположное событию А событие. Элементами события не являются элементы события А.
– элемент f. U – достоверное событие. - невозможное событие.
Если А1, А2,… являются элементами f, то сумма и произведение i-ого количества этих элементов
так же являются элементами f.
Если выполняются пункты 1,2 и 3, то F – поле событий. Если выполняются 1,2,3,4, то F – борелевское поле событий.
Аксиома 1. Каждому случайному событию из поля F ставится в соответствие неотрицательное число Р(А), называемое вероятностью.
Аксиома 2. P(U)=1, следовательно Р(А) меньше или равно 1.
Аксиома 3. Если события А и В несовместны, то Р(А+В)=Р(А)+Р(В).
Аксиома 4.
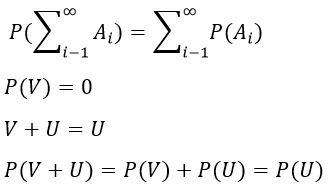
Замечание 1. В аксиоматике Колмогорова понятие события не является первичным, а строится на более элементарных событиях.
Замечание 2. Аксиоматическое построение теории вероятностей отправляется от основных свойств вероятности, подмеченного на примерах классического и статистического определений.
Замечание 3. Система аксиом непротиворечива, т.к. существуют реальные объекты, удовлетворяющие аксиомам.
Замечание 4. Система аксиом не полна. Даже для одного и того же события множества F, вероятности можно выбирать различными способами. Неполнота не является свидетельством их неудачного выбора, а вызвана существом дела.
Каждому случайному событию А из F ставится вероятность Р(А), которую можно рассматривать как функцию. При определении вероятности события А надо иметь множество U, F и функцию Р(А). Совокупность U, F, P(A) называют вероятностным пространством.
При подготовке к экзаменам ориентируйтесь на лекции преподавателя.
Материал взят из моих университетских лекций. Возможны опечатки.
С уважением, Васильева Анна.
