-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение

1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
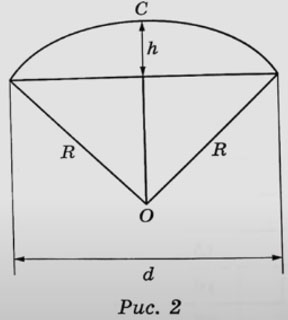
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Представим условие задачи в виде формулы:
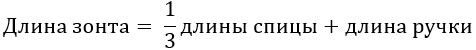
Обозначим длину спицы за х, подставим все величины в формулу и решим получившееся линейное уравнение:
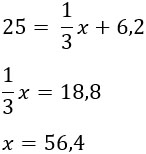
Ответ: 56,4.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Площадь треугольника равна половине произведения основания и высоты, проведенной к этому основанию.
Высота дана и равна 53,1. Основание, а оно же - расстояние между концами соседних спиц, тоже дано и равно 38.
Найдем площадь одного треугольника:
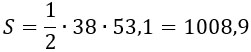
Не забываем, что зонт состоит из восьми таких треугольников, их общая площадь будет равна
1008,9 · 8 = 8071,2.
Осталось округлить это число до десятков. За десятки отвечает цифра 7; после нее стоит цифра 1, значит цифра 7 остается без изменений, а все числа после нее обращаются в 0. Таким образом, 8071,2 ≈ 8070.
Ответ: 8070.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
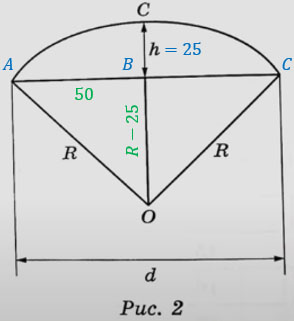
Из условия задачи нам известны h = 25 и d = AC = 100.
Зонт - это симметричная вещица, поэтому АВ = ВС = 50.
Если ОС = R и h = 25, то ОВ = R - 25.
Рассмотрим треугольник АВО. Очевидно, что он прямоугольный. Через теорему Пифагора найдем R:
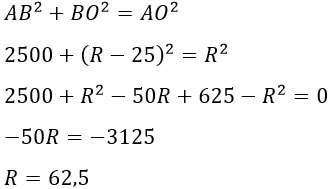
Ответ: 62,5.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
R = 62,5 - из предыдущей задачи;
h = 25 - высота сегмента и высота купола равны между собой.
S = 2 · 3,14 · 62,5 · 25 = 9812,5 ≈ 9813.
Ответ: 9813.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
Один зонт состоит из восьми треугольников, тогда 29 зонтов будут состоять из 232 треугольников.
Если на один треугольник требуется 1050 см2 ткани, то на 232 треугольника нужно будет 1050 · 232 = 243 600 см2.
Площадь ткани в рулоне равна 3500 · 80 = 280 000 см2.
Площадь ткани, ушедшей в обрезки, равна 280 000 - 243 600 = 36 400 см2.
Пусть 280 000 см2 - 100%, а 36 400 - х%. Составим и решим пропорцию:
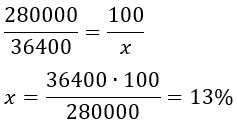
Ответ: 13.
А вы тоже находите проблему из ничего, как Вася и Петя?)
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
| Печь | Тип | Отапливаемый объем, куб. м | Масса, кг | Цена, руб. |
| "Орион" | дровяная | 8-18 | 72 | 15 000 |
| "Огонек" | дровяная | 6-16 | 85 | 23 000 |
| "Плутон" | электрическая | 14-20 | 25 | 18 000 |
1. Найдите объем парного отделения строящейся бани (в куб. м).
2. На сколько рублей дровяная печь, подходящая по отапливаемому объему парного отделения, обойдется дешевле электрической с учетом установки?
3. На сколько рублей эксплуатация дровяной печи, которая подходит по отапливаемому объему парного отделения, обойдется дешевле эксплуатации электрической в течение года?
4. Доставка печи из магазина до участка стоит 800 рублей. При покупке печи ценой выше 20 000 рублей магазин предлагает скидку 5% на товар и 20% на доставку. Сколько будет стоить покупка печи "Огонек" вместе с доставкой на этих условиях?
5. Хозяин выбрал дровяную печь. Чертеж печи показан на рисунке. Размеры указаны в см.
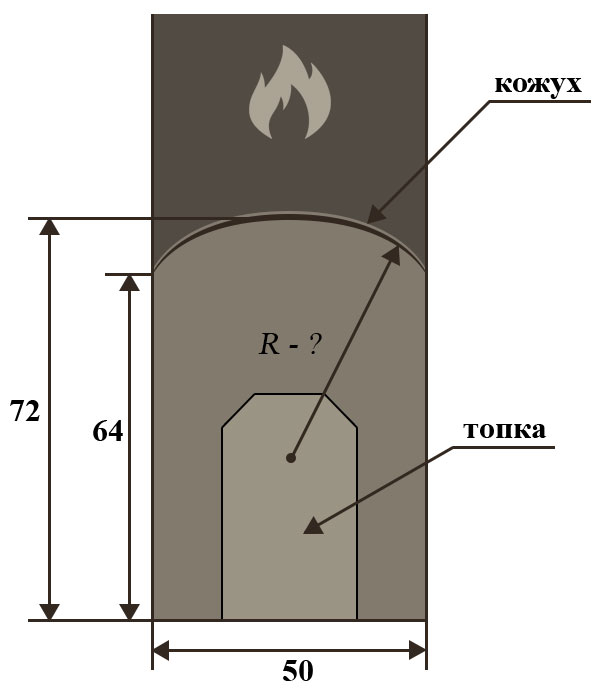
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности. Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха показаны на рисунке. Найдите радиус в сантиметрах; ответ округлите до десятых.
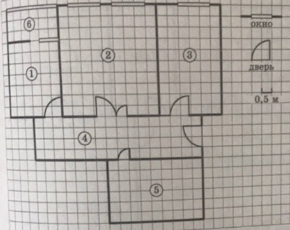
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность пяти цифр.
| Объекты | Спальня | Санузел | Кухня | Гостиная | Прихожая |
| Цифры |
2. Найдите ширину окна в спальне. Ответ дайте в сантиметрах.
3. Плитка для пола размером 25 см х 25 см продается в упаковках по 10 штук. Сколько упаковок плиток понадобится, чтобы выложить пол лоджии?
4. Найдите площадь, которую занимает санузел. Ответ дайте в квадратных метрах.
5. На сколько процентов площадь гостиной больше площади спальни?
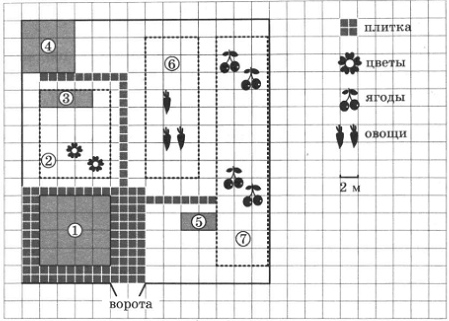
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Объекты | бак | кустарники | жилой дом | баня |
| Цифры |
2. Плиты для садовых дорожек продаются в упаковке по 5 штук. сколько упаковок плит понадобилось, чтобы выложить все дорожки и площадку вокруг дома?
3. Найдите площадь цветника с теплицей. Ответ дайте в квадратных метрах.
4. Найдите суммарную площадь плитки, которой выложены дорожки. Ответ дайте в квадратных метрах.
5. Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
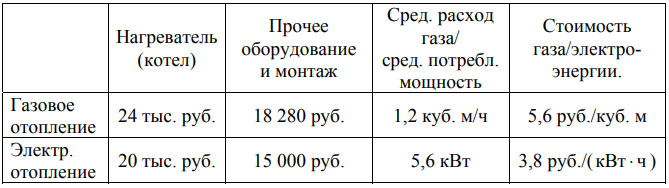
| Нагреватель (котел) | Прочее оборудование и монтаж | Сред. расход газа/сред. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 21 000 руб | 15 269 руб | 1,5 куб. м/ч | 4,3 руб./куб. м |
| Электр. отопление | 15 000 руб | 11 000 руб | 4,8 кВт | 4,4 руб./(кВт·ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости установки газового и электрического оборудования?

Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 30 м, а верхняя точка находится на высоте 5 м от подножия.
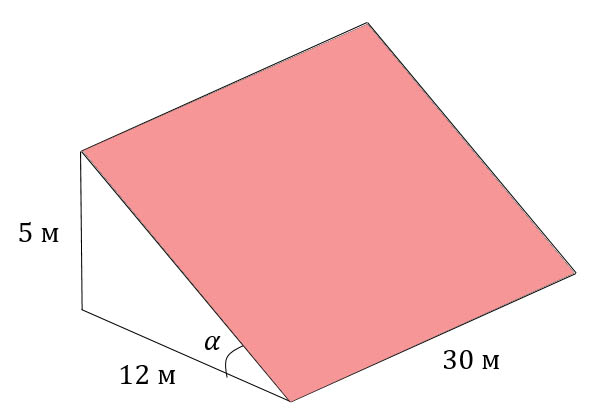
1. Земледелец на расчищенном склоне холма выращивает мускатный орех. Какова площадь, отведенная под посевы? Ответ дайте в квадратных метрах.
2. Земледелец решил устроить террасы на своем участке (см. рисунок ниже), чтобы выращивать рис, пшено и кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона α, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.
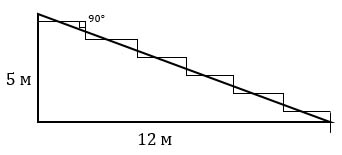
3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
4. Земледелец получает 800 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 22% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
5. В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая - летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Рис | Кукуруза | Пшено | |
| 1-й урожай (июнь) | 600 г/м2 | 1200 г/м2 | не выращивают |
| 2-й урожай (сентябрь) | 800 г/м2 | не выращивают | 300 г/м2 |
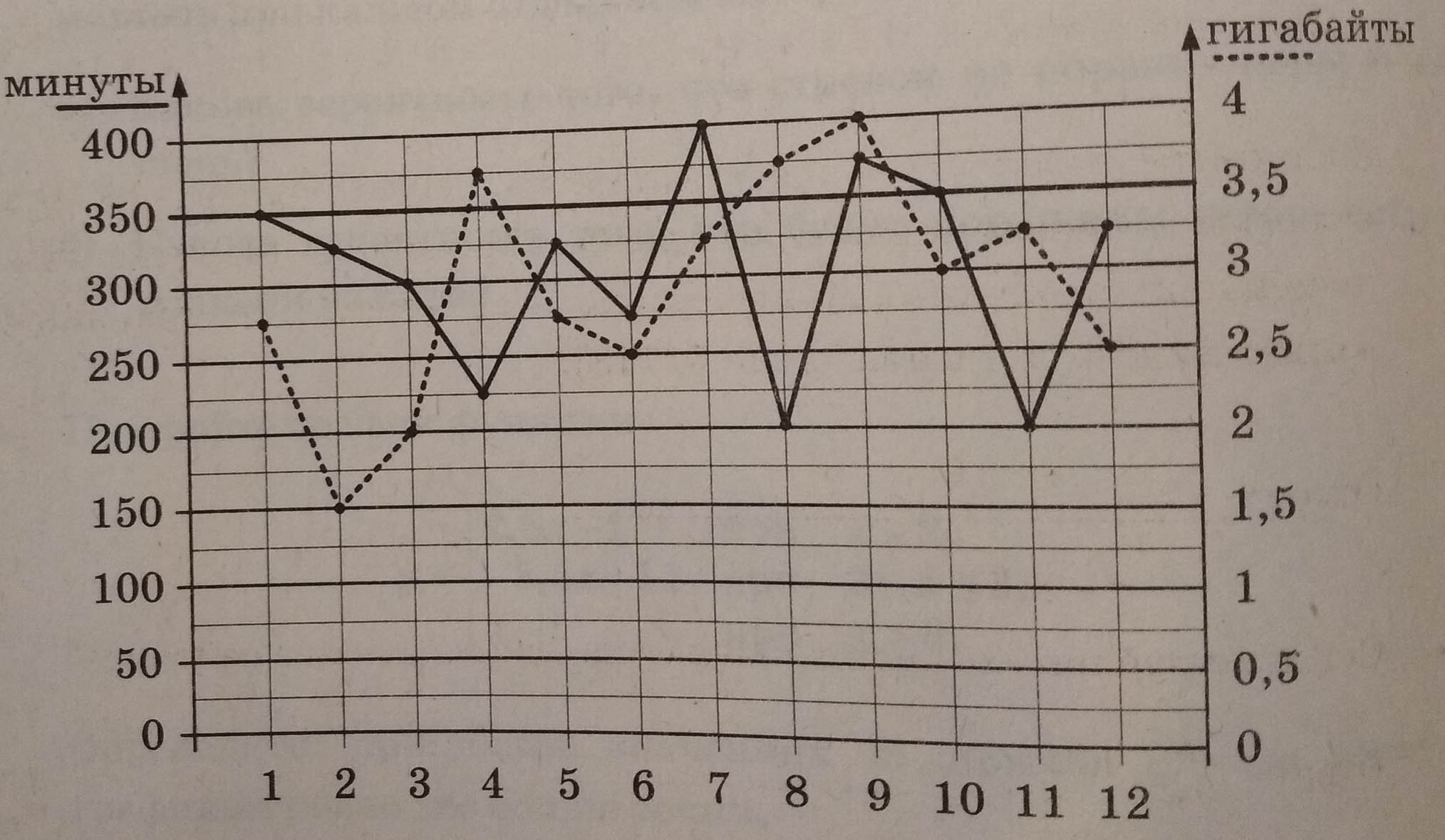
В течение года абонент пользовался тарифом "Стандартный", абонентская плата по которому составляла 300 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа "Стандартный" входит:
- пакет минут, включающий 350 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
- пакет интернета, включающий 3,5 гигабайта мобильного интернета;
- пакет SMS, включающий 150 SMS в месяц;
- безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и SMS сверх сверх пакета указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет | 100 руб. за 0,5 Гб |
| SMS | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 120 SMS.
1. Определите, какие месяцы соответствуют указанному в таблице количеству израсходованных гигабайтов.
| Израсходованные гигабайты | 4 Гб | 1,5 Гб | 2 ГБ | 3 Гб |
| Номер месяца |
Заполните таблицу, в ответ запишите подряд числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для мая, января, ноября, августа, в ответ нужно записать число 51118).
2. Сколько рублей потратил абонент на услуги связи в сентябре?
3. Сколько месяцев в 2018 году абонент не превышал лимит по пакету исходящих минут?
4. Сколько месяцев в 2018 году абонент не превышал лимит ни по пакету минут, ни по пакету мобильного интернета?
5. В конце 2018 года оператор связи предложил абоненту перейти на новый тариф, условия которого приведены в таблице.
| Стоимость перехода на тариф | 0 руб. |
| Абонентская плата в месяц | 350 руб. |
| в абонентскую плату ежемесячно включены: | |
| пакет исходящих минут | 300 минут |
| пакет мобильного интернета | 4 Гб |
| пакет SMS | 150 SMS |
| после расходования пакетов: | |
| входящие вызовы | 0 руб./мин. |
| исходящие вызовы* | 1,5 руб./мин. |
| мобильный интернет | 80 руб. за 0,5 Гб |
| SMS | 3 руб./шт. |
*исходящие вызовы на номера, зарегистрированные на территории РФ
Абонент решает, перейти ли ему на новый тариф, посчитав, сколько бы он потратил на услуги связи в 2018 г., если бы пользовался им. Если получится меньше, чем он потратил фактически за 2018 г., то абонент примет решение сменить тариф.
Перейдет ли абонент на новый тариф? В ответ запишите ежемесячную абонентскую плату по тарифу, который выберет абонент на 2019 год.
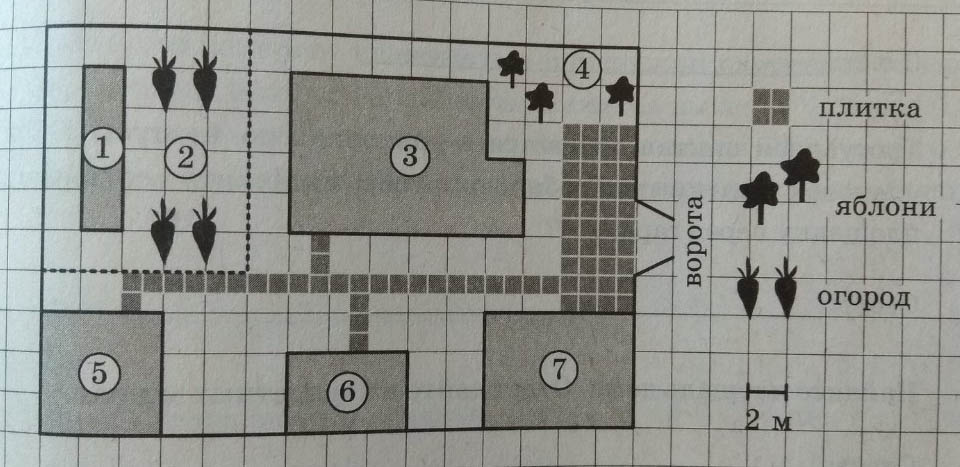
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.

2. Тротуарная плитка продается в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Найдите площадь дома. Ответ дайте в квадратных метрах.
4. Найдите расстояние от сарая до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
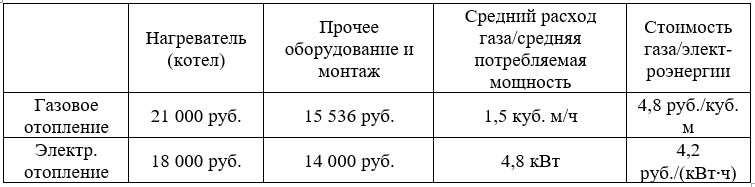
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости установки газового и электрического оборудования?
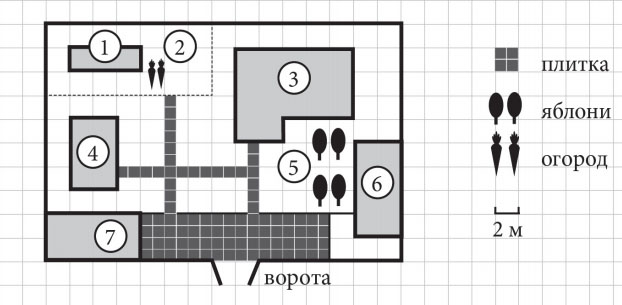
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

2. Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
4. Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
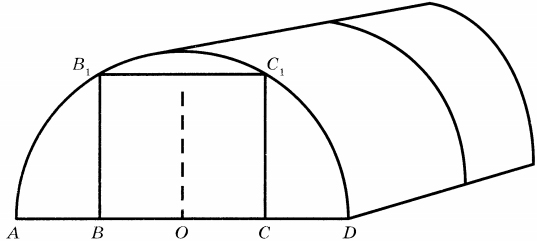
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
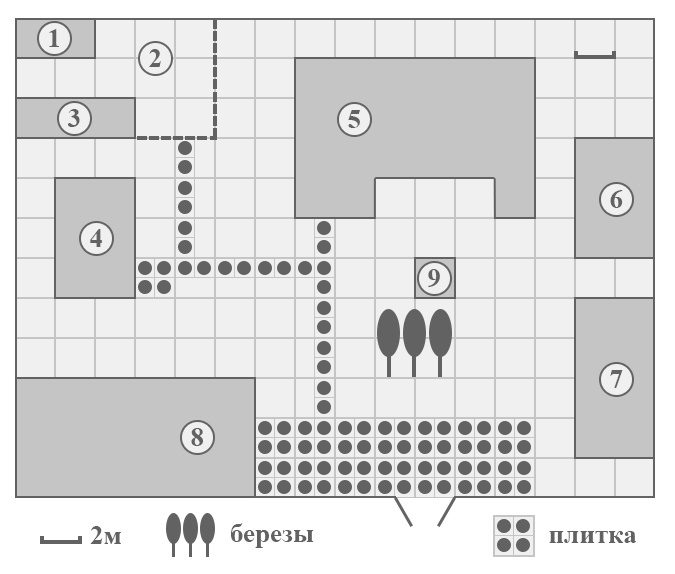
1. Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | жилой дом | компостная яма | фонтан | баня | теплица |
| Цифры |
2. Тротуарная плитка продается в коробках по 15 штук. Сколько коробок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
3. Найдите площадь, которую суммарно занимают жилой дом и баня. Ответ дайте в квадратных метрах.
4. Найдите расстояние от бани до теплицы (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
5. Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трех поставщиков плитки.
| Поставщик | Стоимость плитки (в рублях за кв.м) | Доставка (в рублях) | Работы по демонтажу старой плитки и по укладки новой (в рублях) |
| 1 | 500 | 3000 | 2500 |
| 2 | 500 | 4000 | бесплатно |
| 3 | 555 | бесплатно | 3500 |
Во сколько рублей обойдется владельцам выгодный вариант?

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Объекты | Баня | Гараж | Сарай | Теплица |
| Цифры |
2. Тротуарная плитка продается в упаковках по 3 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки?
3. Найдите площадь открытого грунта огорода вне теплицы. Ответ дайте в квадратных метрах.
4. Сколько процентов площади всего участка занимает огород?
5. Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котел) | Прочее оборудование и монтаж | Средний расход газа/средняя потребляемая мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 25 000 рублей | 17 552 рублей | 1,3 куб. м/ч | 5,2 руб./куб. м |
| Электр. отопление | 21 000 рублей | 15 000 рублей | 5,2 кВт | 4,1 руб./(кВт·ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости установки газового и электрического оборудования?
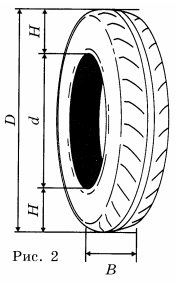
1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.
2. На сколько миллиметров радиус колеса с маркировкой 195/60 R14 больше, чем радиус колеса с маркировкой 165/70 R14?
3. Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
4. На сколько миллиметров уменьшится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/45 R16?
5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/55 R15? Округлите результат до десятых.

Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 50 м, а верхняя точка находится на высоте 16 м от подножия.
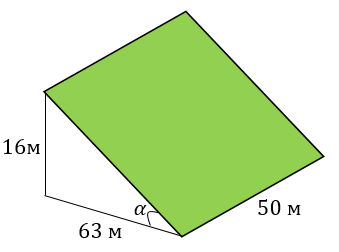
1. Земледелец на расчищенном склоне холма выращивает мускатный орех. Какова площадь, отведенная под посевы? Ответ дайте в квадратных метрах.
2. Земледелец решил устроить террасы на своем участке (см. рисунок ниже), чтобы выращивать рис, пшено и кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона α, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.
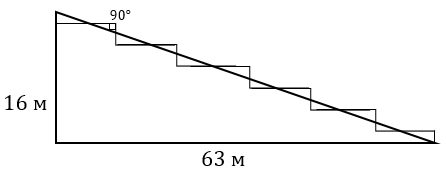
3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
4. Земледелец получает 700 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 14% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
5. В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая - летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Рис | Кукуруза | Пшено | |
| 1-й урожай (июнь) | 700 г/м2 | 600 г/м2 | не выращивают |
| 2-й урожай (сентябрь) | 600 г/м2 | не выращивают | 650 г/м2 |
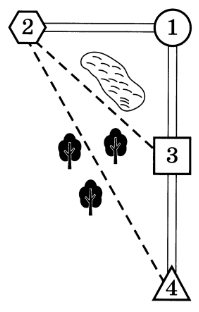
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Населенные пункты | д. Березовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры |
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
3. Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минут потратят на дорогу Миша с дедушкой, если проедут этим маршрутом.

Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 20 м, а верхняя точка находится на высоте 7 м от подножия.
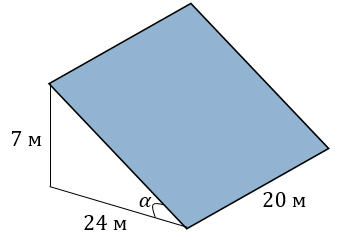
1. Земледелец на расчищенном склоне холма выращивает мускатный орех. Какова площадь, отведенная под посевы? Ответ дайте в квадратных метрах.
2. Земледелец решил устроить террасы на своем участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона α, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.
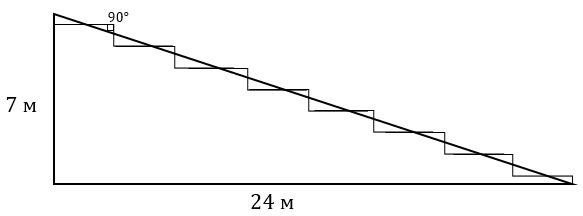
3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы?
4. Земледелец получает 750 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 18% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
5. В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая - летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Рис | Кукуруза | Пшено | |
| 1-й урожай (июнь) | 700 г/м2 | 800 г/м2 | не выращивают |
| 2-й урожай (сентябрь) | 750 г/м2 | не выращивают | 500 г/м2 |
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
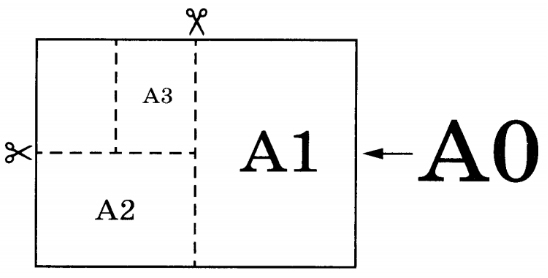
1. Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А3 | А4 | А5 | А6 |
2. Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
3. Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата АЗ. Ответ дайте в квадратных сантиметрах.
5. Найдите отношение длины большей стороны листа к меньшей у бумаги формата А1. Ответ дайте с точностью до десятых.