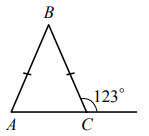
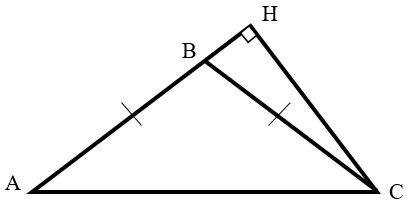
-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
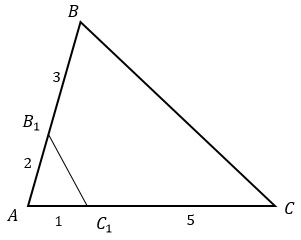
Если АВ = 5, а ВВ1 = 3, то АВ1 = 5 - 3 = 2.
Если АС1 = 1, а СС1 = 5, то АС = 1 + 5 = 6.
Запишем формулы для нахождения площадей треугольников АВ1С1 и АВС через синус их общего угла А:
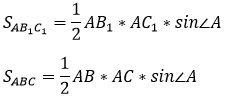
Но не просто так нам дана площадь четырехугольника. Используя ее можно выразить площадь маленького треугольника через разность большого треугольника и этого четырехугольника. Запись будет выглядеть так:
![]()
Преобразуем это равенство через формулы, которые мы написали выше:
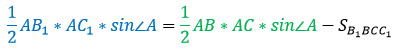
Подставим все известные величины и решим уравнение относительно синуса угла А.
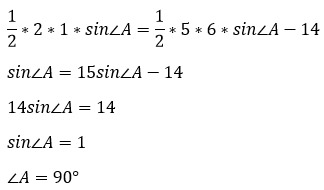
Опачки! Треугольники оказались прямоугольными!
Площадь прямоугольного треугольника равна половине произведения его катетов, т.е.
![]()
Ответ: 1.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.