Биссектрисы углов C и D трапеции ABCD пересекаются в точке Р, лежащей на стороне АВ. Докажите, что точка P равноудалена от прямых ВС, CD и AD.

Самое грустное тут - нарисовать чертеж. А хороший чертеж - залог успеха!) Вот, что вышло у меня:

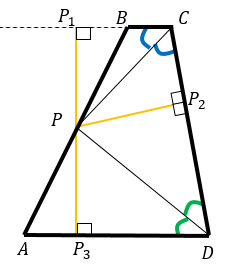
Проведем из точки Р перпендикуляры к прямым ВС (придется ее продолжить), СD и AD. На чертеже они нарисованы оранжевым цветом. Если окажется, что PP₁ = PP₂ = PP₃, то точка Р будет равноудалена от всех перечисленных выше прямых.

Докажем, что это действительно так.

1) Рассмотрим прямоугольные треугольники СРР₁ и СРР₂: СР - общая, Р₁СР = РСР₂ (СР - биссектриса). Получается, что треугольники равны по гипотенузе и острому углу. А из равенства треугольников следует, что РР₁ = РР₂.

2) Рассмотрим прямоугольные треугольники DРР₂ и DРР₃: DР - общая, Р₃DР = РDР₂ (DР - биссектриса). Получается, что треугольники равны по гипотенузе и острому углу. А из равенства треугольников следует, что РР₂ = РР₃.

3) Если РР₁ = РР₂ и РР₂ = РР₃, то РР₁ = РР₃.

Следовательно, точка Р равноудалена от прямых ВС, CD и AD.

Что и требовалось доказать.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.