-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
Дано:
S - сумма кредита
а = 20% = 0,2
m = 1 + 20/100 = 1,2 (про полезный коэффициент читай тут)
Общая сумма выплат < 9 млн
Найдите: Sнаиб.
Решение:
1 год. Сумма кредита S увеличивается в 1,2 раз (на 20%) и выплачивается только процент по кредиту, т.е.
1,2S - 0,2S = S (я не буду выводить формулу, по которой мы сразу сможем найти S потому, что она получится слишком лихой; конкретно в этой задаче проще сразу подставлять нужные значения)
2 год. Аналогично с первым: увеличение суммы и выплата процентов:
1,2S - 0,2S = S.
3 год. Ничего не меняется, все также:
1,2S - 0,2S = S.
4 год. Здесь становится немного веселее, т.к. наконец-то происходит выплата части денег. И, конечно, про увеличение долга на 20% не забываем!
1,2S - x.
5 год. На оставшуюся сумму долга накладываем проценты, делаем точно такую же выплату, как и на 4-от году, и погашаем кредит:
1,2(1,2S - x) - х = 0;
1,44S - 1,2x - x = 0;
2,2x = 1,44S;
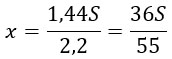
Мы выразили х - выплату, которую производят на 4-ом и на 5-ом годах кредитования.
Но помимо этих двух выплат были еще выплаты процентов по кредиту. Просуммируем их и найдем общую суммы выплат в течение пяти лет:
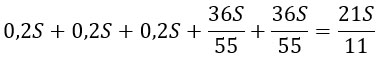
В задаче сказано, что общая сумма выплат должна быть меньше 10 млн, т.е.
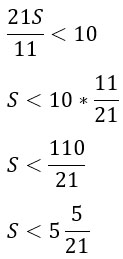
Кредит берется на целое число миллионов, размер кредита должен быть наибольшим, значит, S = 5 млн.
Ответ: 5000000 рублей.