-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
Если видишь в условии задачи фразу "на одну и ту же", то это задача на дифференцированный платеж. О разнице аннуитетного и дифференцированного платежах можно посмотреть здесь на примерах двух задач.
Распишем, что дано.
S - сумма денег, взятая в кредит
а = 2
n = 24 месяца
m = 1 + 2/100 = 1,02 (полезный коэффициент; увеличитель суммы долга)
xn - ежемесячные выплаты
х1 + ... + х12 = 1 370 000 руб.
S - ?
Решение:
Если долг на одну и ту же величину меньше, то это говорит о том, что он уменьшается равномерно каждый месяц на S/24 (всю сумму кредита S разделили на 24 месяца).
Помимо этого мы знаем, что каждый месяц долг увеличивается на 2% (в m раз) и делается выплата.
Распишем, что будет происходить с долгом по месяцам (Нас будут интересовать только 1-й и 12 -й месяцы).
Помимо того, что я распишу изменение суммы долга, я сразу выражу выплаты, которые должны будут производиться.
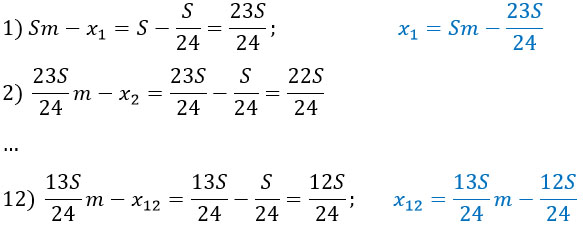
Небольшой комментарий к предыдущей записи. Я не случайно расписала изменение долга за второй месяц. Именно он позволяет мне перепрыгнуть сразу к 12-ому месяцу. Как так получается? Номер второго месяца и числитель в первой дроби в сумме дают 25 (2 + 23), и такая сумма должна быть и в 3-ем, 4-ом, ..., 12-ом, ..., 24-ом месяцах. Если мой месяц идет под номером 12, то в числителе будет стоять число 13, т.к. 12 + 13 = 25.
Как мы уже знаем, долг уменьшается равномерно на одну и ту же сумму, т.е. уменьшается в арифметической прогрессии.
Выразим сумму выплат за первые 12 месяцев по формуле суммы первых n членов арифметической прогрессии. В оригинале формула выглядит так:
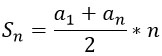
Адаптируя ее под нашу задачу, получим такую:
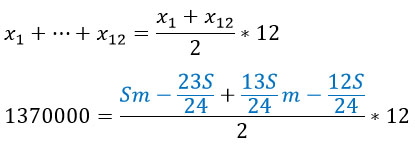
Путем несложных преобразований найдем S.
0,685S = 1370000;
S = 2 000 000
Ответ: 2 000 000 рублей.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.