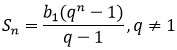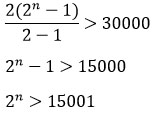Митя играет в компьютерную игру. Он начинает с 0 очков, а для перехода на следующий уровень ему нужно набрать не менее 30 000 очков. После первой минуты игры добавляется 2 очка, после второй – 4 очка, после третьей – 8 очков и так далее. Таким образом, после каждой следующей минуты игры количество добавляемых очков удваивается. Через сколько минут Митя перейдет на следующий уровень?
Решение:
Пусть
b1 = 2 - количество очков, набранных за первую минуту игры,
b2 = 4 - количество очков, набранных за вторую минуту,
b3 = 8 - количество очков, набранных за третью минуту,
.......
bn - количество очков, набранных за последнюю минуту.
Количество очков постоянно удваивается, значит дело мы имеем с геометрической прогрессией со знаменателем q = 2.
Каждую минуту очки суммируются, т.е. актуальна будет формула суммы первых n членов прогрессии. Формула выглядит так:
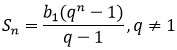
К тому же, эта сумма должна быть не меньше 30 000.
Подставляя известные величины в формулу, получим такое неравенство:
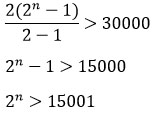
Ничего не остается, как вручную подобрать n.
При n = 14 выражение 2n будет больше 15 001 (214 = 16384). Это значит, что через 14 минут Митя наберет больше 30 000 очков и перейдет на следующий уровень.
Ответ: 14.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#839
ТОП 15 примеров из раздела "Прогрессии"
Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?
#357
В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7-й день акция стоила 999 рублей, а в 12-й день - 1064 рубля.
#838
Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 9 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?
#871
Митя играет в компьютерную игру. Он начинает с 0 очков, а для перехода на следующий уровень ему нужно набрать не менее 30 000 очков. После первой минуты игры добавляется 2 очка, после второй – 4 очка, после третьей – 8 очков и так далее. Таким образом, после каждой следующей минуты игры количество добавляемых очков удваивается. Через сколько минут Митя перейдет на следующий уровень?
#839
При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется 0,5 г осадка. Найдите массу осадка (в граммах) в растворе спустя восемь минут после начала реакции.
#835
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние меньше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в сумме 9,5 метра. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 57 метрам.
#837
Миша решил заказать себе такси. Подача машины и первые 5 минут поездки в совокупности стоят 159 рублей, а стоимость каждой следующей минуты фиксирована. Стоимость поездки с 6 по 15 минуту (включительно) составила 80 рублей, а с 6 по 25 минуту - 160 рублей. Найдите итоговую стоимость поездки, если поездка длилась 1 час.
#832
У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 15 см?
#870
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 7 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты. Ответ дайте в миллиграммах.
#865
Грузовик перевозит партию щебня массой 270 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 6 тонны щебня. Определите, сколько тонн щебня было перевезено на шестой день, если вся работа была выполнена за 12 дней.
#833
Для получения витамина D могут быть рекомендованы солнечные ванны. Загорать лучше утром до 10 часов или вечером после 17 часов. Виктору назначили курс солнечных ванн. Виктор начинает курс с 15 минут в первый день и увеличивает время этой процедуры в каждый следующий день на 6 минут. В какой по счету день продолжительность процедуры достигнет 1 часа 15 минут?
#848
На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 120.
#868
При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 6° C. Найдите температуру вещества (в градусах Цельсия) через 4 минуты после начала проведения опыта, если его начальная температура составляла − 7° C.
#869
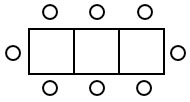
Ира зовет гостей на день рождения в ресторан. В ресторане в наличии имеются лишь квадратные столики, за которыми умещается не более 4 человек. Если соединить два квадратных стола, то получится стол, за которым умещается до 6 человек. На рисунке изображен случай, когда соединили 3 квадратных столика. В этом случае получился стол вместимостью до 8 человек. Найдите наибольшую вместимость стола, который получится при соединении 14 квадратных столиков в ряд.
#834
В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 13 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.
#866