В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.

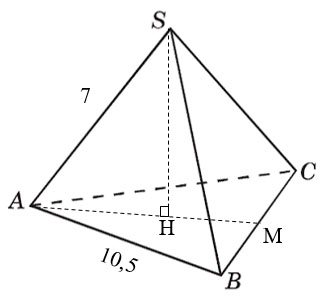
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Проведем медиану AM. Т.к. медиана делит сторону пополам, то BM=10,5:2=5,25. В равностороннем треугольнике медиана так же является и высотой, значит треугольник ABM – прямоугольный. Найдем АМ по теореме Пифагора. Удобно считать не в десятичных дробях, а в обыкновенных, поэтому

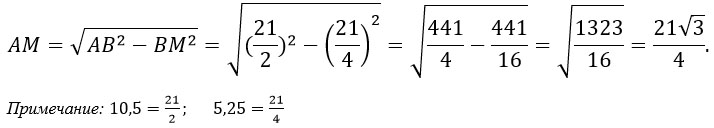
Если мы проведем все три медианы, то они пересекутся в точке Н. По свойству медиан в треугольнике, точка их пересечения делит отрезки AH и HM в отношении 2:1, начиная от вершины. Это значит, что чтобы найти АН надо вычислить 2/3 от АМ.

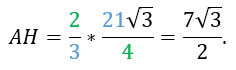
Треугольник SAH – прямоугольный. Найдем SH по теореме Пифагора. 

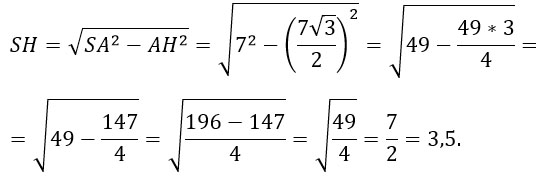
Ответ: 3,5.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.