Сторона CD параллелограмма ABCD вдвое больше стороны AD. Точка Р - середина стороны CD. Докажите, что АР - биссектриса угла BAD.

Для удобства введем обозначения:

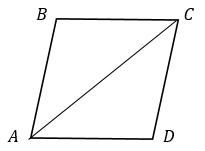
пусть AD = CB = x, тогда СD = AB = 2х.

Т.к. Р - середина CD, то CP = PD = x.

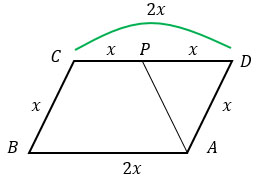
Рассмотрим треугольник PDA: он равнобедренный, т.к. PD = DA = x, следовательно, углы DPA и DAP равны (углы при основании).

Также равны углы DPA и PAВ как накрест лежащие при пересечении параллельных прямых CD и АВ секущей АР.

Отсюда следует, что ∠DAP = ∠PAВ и АР является биссектрисой угла DAB.

Что и требовалось доказать.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.