Докажите, что диагонали параллелограмма разделяют его на 4 равновеликих треугольника.

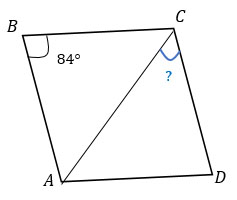
Равновеликие - значит с одинаковой площадью.

Диагонали параллелограмма точкой пересечения делятся пополам.

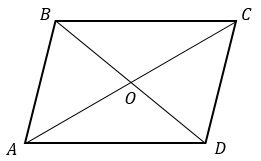
Треугольники ВОС и AOD равны: ВО = OD, AO = OC, ∠BOC = ∠AOD - вертикальные.

Треугольники AOB и COD равны равны по той же причине: ВО = OD, AO = OC, ∠AOB = ∠COD - вертикальные.

Площади равных треугольников равны, значит, для решения этой задачи достаточно доказать, что равны площади двух смежных треугольников. Я возьму треугольники AOB и ВСО.

Выразим площади этих треугольников через 2 стороны и синус угла между ними:

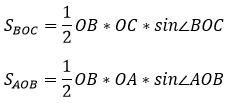
Т.к. ОС = ОА (две половинки одной диагонали) и sin∠BOC = sin∠AOB (Синусы смежных углов равны. Очень клёвое свойство, доказывается через формулу приведения), то площади этих треугольников будут равны, а значит, что и все четыре треугольника будут иметь одинаковую площадь.

Что и требовалось доказать.