-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение

Квадратное неравенство будет иметь решения, если его дискриминант больше или равен нулю.
Поэтому находим те неравенства, в которых дискриминант меньше 0.
Попробуем первое неравенство:
D = b2 - 4ac = 81 - 4 · (-79) > 0.
Первое неравенство имеет решение, как впрочем и четвертое. Их отметаем.
Найдем дискриминант второго неравенства.
D = b2 - 4ac = 81 - 4 · 79 < 0. То, что надо!
Т.к. левая часть третьего неравенства такая же, то и у него дискриминант также отрицателен.
Какое же неравенство не будет иметь решений: 2 или 3?
Обратимся к графическому методу.
Схематично начертим график функции y = x2 + 9x + 79.
Графики этих неравенств - параболы, ветви направлены вверх. Дискриминант меньше 0, значит график ось Ох не пересекает и расположен следующим образом:
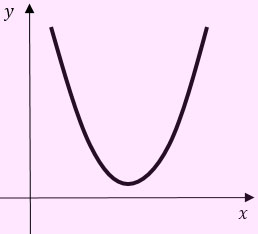
Т.к. y = x2 + 9x + 79 и x2 + 9x + 79 > 0, то у > 0. Можем ли мы по чертежу найти значения положительных y взяв любое число по оси Ох? Можем!
Значит неравенство 2) имеет решения.
А вот неравенство 3) решений не имеет. Это видно и по чертежу: мы не сможем подобрать число по оси Ох так, чтобы значение y было отрицательным.
Ответ: 3.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.


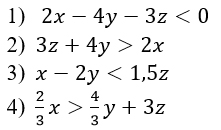
Укажите решение неравенства х2-36>0.
1) (-∞; +∞) 2) (-6; 6) 3) (-∞; -6)∪(6; +∞) 4) нет решений