-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
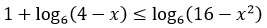
Перенесем логарифмы в одну сторону, число в другую.
![]()
По свойству логарифмов их разность равна логарифму частного.
![]()
Разложим числитель дроби по формуле "Разность квадратов": a2 - b2 = (a - b)(a + b). Единицу представим как логарифм по основанию 6 числа 6, т.к. 61 = 6.
![]()
Дробь сокращаем на (4 - х), откидываем логарифмы (потому что у них одинаковое основание) и получаем простейшее неравенство.
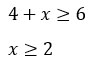
Но не всё так просто. Ни в коем случае нельзя забывать про ОДЗ.
Т.к. мы ранее сокращали дробь на (4 - х), то х ≠ 4 (знаменатель не может равняться 0).
Помимо этого по определению логарифма logab b должен быть больше нуля.
Решим следующее неравенство для определения ОДЗ: 16 - х2 > 0.
Раскладываем на множители: (4 - x)(4 + x) > 0.
Методом интервалов находим положительные промежутки. Это и будет областью допустимых значений.
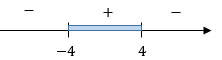
Применяя ОДЗ для нашего ответа получаем, что х ∈ [2; 4).
Ответ: [2; 4).
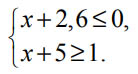


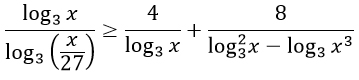
Укажите решение неравенства х2-36>0.
1) (-∞; +∞) 2) (-6; 6) 3) (-∞; -6)∪(6; +∞) 4) нет решений