-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
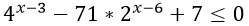
Типичное показательное неравенство, одно из самое простых, попалось мне сегодня для решения.
Воспользуемся свойством степеней an : am = an-m, четверку представим как 2 в квадрате и преобразуем левую часть неравенства. Вот что получится:
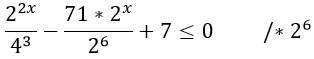
Домножим обе части неравенства на общий знаменатель 26.
![]()
Замена. Пусть 2х = t, тогда
![]()
Разложим левую часть неравенства на множители по формуле ax2 + bx + c =a(x - x1)(x - x2), для этого найдем корни квадратного трехчлена.
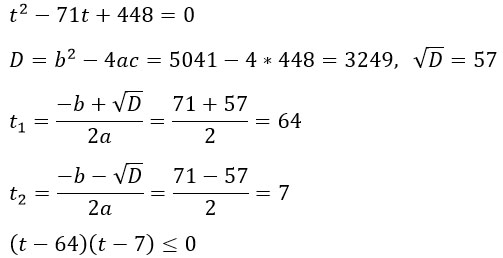
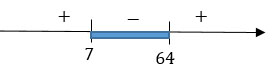
Решим это неравенство методом интервалов.
Знаки промежутков определяются таким образом: из самого левого промежутка берем какое-нибудь число, например, 65, и подставляем в левую часть неравенства; считаем; определяем знак результата - положительный; ставим плюс. Далее берем число из среднего промежутка, например, 10. Подставляем в левую часть и видим, что результат отрицательный. Ставим минус. Аналогично действуем с правым промежутком.
В заключении надо сказать, что знак неравенства у нас "меньше или равно", поэтому нас интересует только промежуток со знаком "минус".
Итак, t принадлежит промежутку [7; 64]. Запишем это так:
![]()
Делаем обратную замену и находим х.
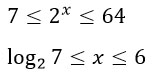
Ответ: х ∈ [log27; 6]
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.


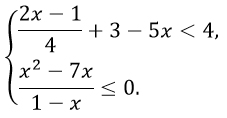
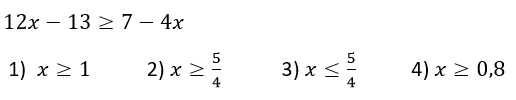
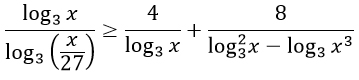
Укажите решение неравенства х2-36>0.
1) (-∞; +∞) 2) (-6; 6) 3) (-∞; -6)∪(6; +∞) 4) нет решений