-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
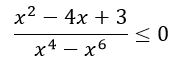
Перед тем как решать данное неравенство надо разложить числитель на множители. Знаменатель не трогаем: с ним все отлично, он уже почти разложен как надо. Формула разложения квадратного трехчлена на множители выглядит так:
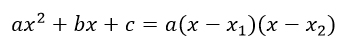
Чтобы ей воспользоваться, необходимо приравнять числитель к 0, найти корни получившегося квадратного уравнения и подставить их в формулу.
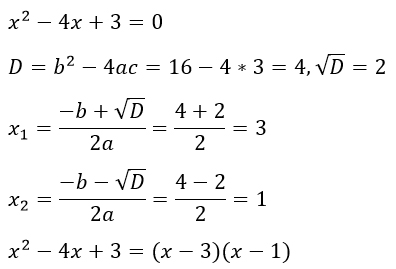
Теперь разложенный трехчлен записываем в числитель. В знаменателе видим формулу сокращенного умножения "разность квадратов". Раскладываем. Замечаем, что в числителе и знаменателе есть противоположные множители: (x - 1) и (1 - x). Их можно сократить поменяв знак неравенства, как я, или с помощью вынесения минуса из какой-то из этих скобок. В итоге все равно придется умножать на -1 для удобства и менять знак неравенства. (Если манипуляции с этим не понятны, то я распишу подробнее в комментариях, только скажите :) )
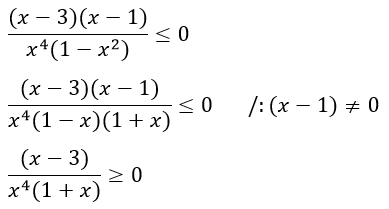
Чертим координатную прямую. Отмечаем на ней точки, значения дроби в которых равны 0. Иными словами устно решаем три уравнения x - 3 = 0, x4 = 0 и 1 + x = 0. Их результаты и пойдут на наш чертеж. Причем, точки -1 и 0 будут выколотыми, т.к. знаменатель дроби не может быть равен нулю.
На экзамене никогда не ставьте автоматом знаки + и -. Обязательно проверьте каждый интервал!!
Обычно начинают проверять знак дроби с правого интервала. Этот пример не будет исключением. Из промежутка от 3 до плюс бесконечности берем, например, число 4. Подставляем его в нашу дробь вместо икса (подстановка идет не в ту дробь, которая была в начале, а в ту, которую мы получили после преобразований!) , считаем (можно, кстати, не считать, а просто прикинуть положительная дробь будет или нет). Дробь будет положительна, значит на чертеже ставим "+". Из интервала от 0 до 3 возьмем 1. Так же подставляем: дробь отрицательна. И т.д.
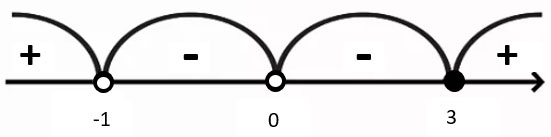
Смотрим на знак нашего неравенства: больше или равно. Значит нас интересуют те интервалы, в которых дробь больше или равна 0, т.е. положительна. Смотрим туда, где плюсики стоят. В ответ записываем объединение промежутков.
Ответ: (-∞; -1) ∪ [3; +∞).
P.S. у бесконечностей всегда круглые скобки.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.


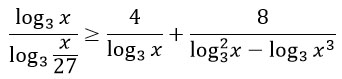
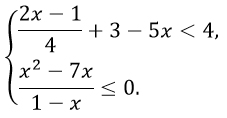
Укажите решение неравенства х2-36>0.
1) (-∞; +∞) 2) (-6; 6) 3) (-∞; -6)∪(6; +∞) 4) нет решений