В выпуклом четырехугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

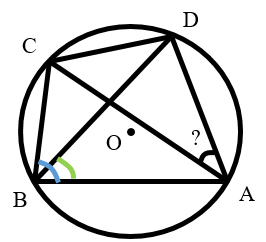
Задача состоит в том, чтобы доказать равенство углов-звездочек.

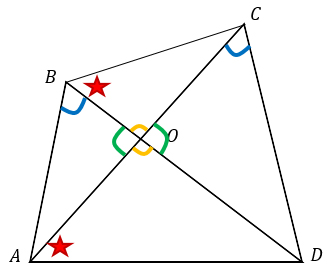
1) Треугольники АВО и CDO подобны по двум углам, т.к. ∠АВО = ∠DCO по условию, а ∠ВОА = ∠СОD - вертикальные. Из подобия треугольников следует пропорциональность сходственных сторон: 

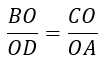
2) Треугольники ВОС и AOD подобны по двум пропорциональным сторонам и углу между ними, т.е.   и ∠BOC = ∠AOD - вертикальные. Из подобия треугольников следует равенство их соответствующих углов, значит, ∠DBC = ∠DAC.

Что и требовалось доказать.