На рисунке изображен график y=f'(x) – производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна оси абсцисс или совпадает с ней.

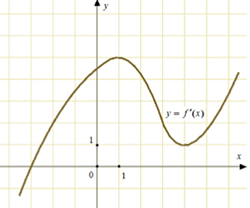
Ось Ох имеет угловой коэффициент k = 0, следовательно и касательная к графику будет иметь коэффициент k = 0.

При этом производная функции f(x) равна угловому коэффициенту (геометрический смысл производной), т.е. f'(x) = k или f'(x) = 0.

Проведем эту линию на рисунке и найдем точку пересечения графика с этой прямой.

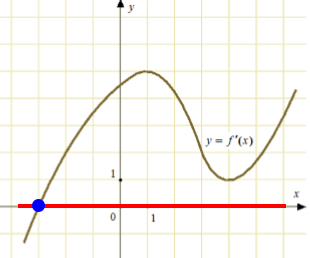
Это и будет абсцисса точки, в которой касательная к графику параллельна оси Ох или совпадает с ней.

Ответ: -3.