На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки −2, −1, 2, 3. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

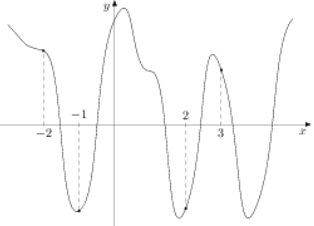
Проведем касательные к графику через предложенные точки.

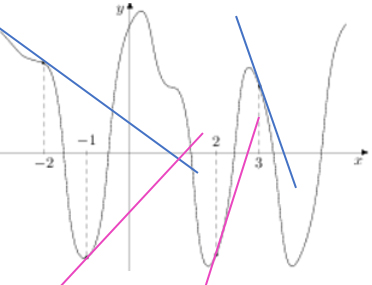
Касательная - это прямая, которая задается формулой y = kx + b, где k - угловой коэффициент.

Геометрический смысл производной состоит в том, что производная функции f(x) равна угловому коэффициенту касательной к оси Ох.

Синие касательные направлены вниз, значит их угловой коэффициент k отрицательный, следовательно и производная функции будет отрицательна. А нам надо наибольшее значение, поэтому точки -2 и 3 отбрасываем.

Розовые касательные направлены вверх, значит их угловой коэффициент k положительный, следовательно, производная будет положительна.

Сравним углы. Т.к. нам нужно наибольшее значение производной, то выбираем касательную с наибольшим углом наклона: эта касательная проходит через точку с абсциссой 2.

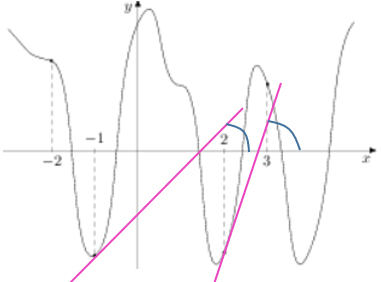
Ответ: 2.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.